日常算法总结
完全二叉树插入
问题描述
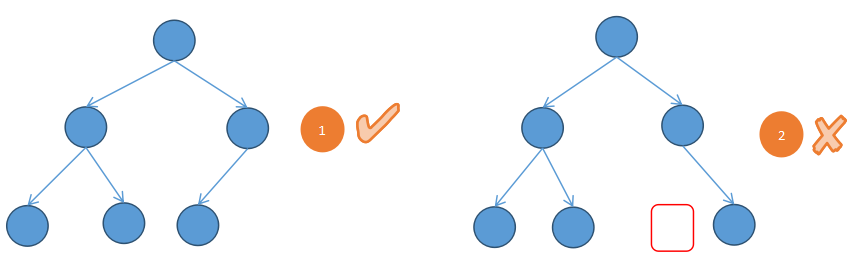
已知一个完全二叉树的结构,现在需要将一个节点插入到这颗完全二叉树的最后,使得它还是一个完全二叉树。
第一种解法:如果该树为满二叉树或者左子树不为满二叉树,那么就进入左子树,否则进入右子树,递归进行。
二叉树(Binary Tree)
** 二叉树** 任何一个节点的子节点数量不超过2
完全二叉树
- 所有叶子结点都在最后一层或倒数第二层。
- 最后一层的叶子结点在左边连续,倒数第二节的叶子结点在右侧连续。
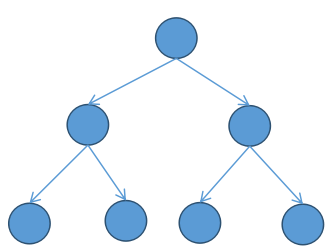
** 满二叉树 **
- 所有叶子结点都在最后一层
- 结点的总数为 $2^n -1$ (n 为树的高度)
满二叉树是一种特殊的完全二叉树
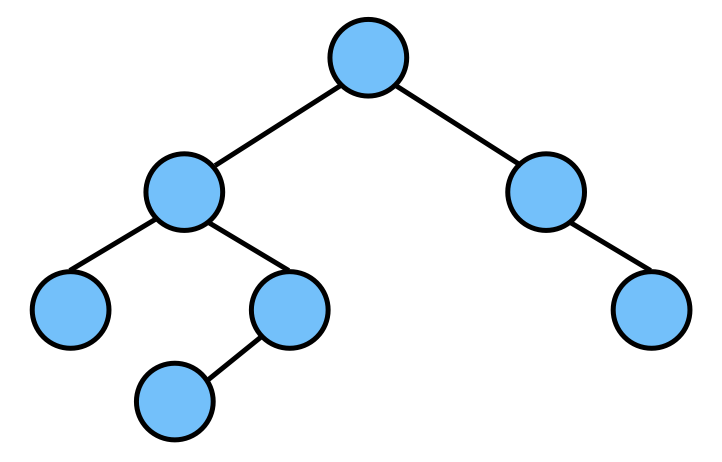
平衡二叉树 也叫 AVL 树
- 它是一颗空树或左右两个子树的高度差的绝对值不超过1。
- 左右两个子树均为平衡二叉树。
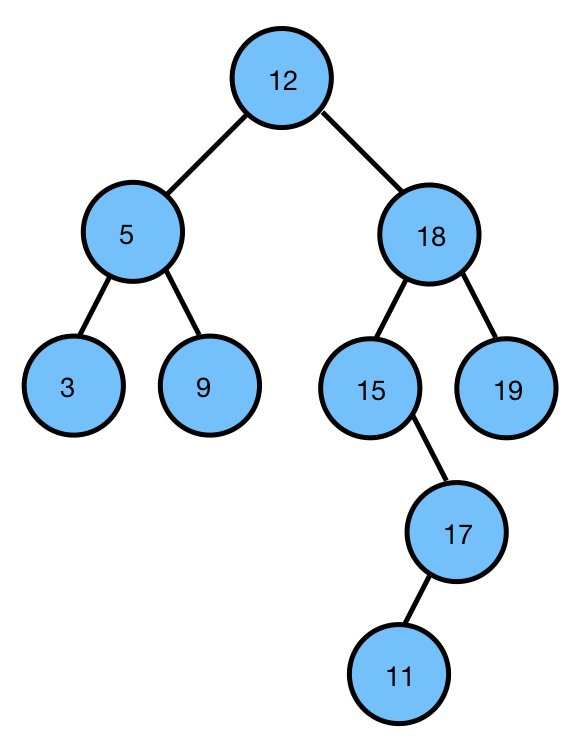
**二叉搜索树(Binary Search Tree) ** 也叫二叉查找树、二叉排序树
- 若子树不空,则子树上所有节点的值均小于或等于根节点的值。
- 若右子树不空,则右子树所有节点的值均大于或等于根节点的值。
- 左、右子树也分别为二叉排序树,或是一颗空树。
** 哈夫曼树**
带权路径长度达到最小的二叉树,也叫做最优二叉树。
树的深度和高度:深度是从上往下数;高度是从下往上数
代码实现
平滑过渡到本问题的代码实现。树的高度就是树的遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
#include<iostream>
using namespace std;
typedef struct Node{
int value;
struct Node *lchild, *rchild;
}Tree;
int GetLeftDepth(Tree* root){
Tree* pNode =root->lchild ;
int depth =0;
while(pNode != NULL)
{
depth ++;
pNode =pNode->lchild;
}
return depth;
}
int GetRightDepth(Tree* root){
Tree* pNode =root->rchild;
int depth =0 ;
while(pNode != NULL)
{
depth ++ ;
pNode =pNode->rchild ;
}
return depth;
}
bool IsFullBinaryTree(Tree* root)
{
return GetLeftDepth(root) == GetRightDepth(root) ;
}
void insert(Tree* root, Tree * node){
if (IsFullBinaryTree(root) || !IsFullBinaryTree(root->lchild)){
insert(root->lchild, node);
return ;
}
if (root->rchild ==NULL){
root->rchild =node ;
return ;
}
insert(root->rchild, node) ;
}
int main()
{
Node* a = new Node();
a->value =1;
}
|
inplace 去除连续的 0
给定一个一维整数数组,不使用额外的空间,本地去掉数组中连续的0。
Tips: 前后两个指针,判断是否是连续的0。第三个指针标记新的数组,前者覆盖后者。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include<iostream>
using namespace std;
int RemoveDuplicates(int* sortBuffer,int length)
{
if(sortBuffer == NULL || length == 0)
{
return false;
}
int count = 0;
for(int i = 1; i < length; i++)
{
if(sortBuffer[i] ==0 && 0 == sortBuffer[i-1])
{
continue;
}
else
{
sortBuffer[count]=sortBuffer[i];
count++;
}
}
return count;
}
int main()
{
int length =sizeof(array)/sizeof(int);
}
|
最大连续子数组和
已知一个整数二维数组,求最大的子数组和(子数组的定义从左上角(x0,y0) 到右下角(x1,y1)的数组)
先考虑一维整数数组的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#include<iostream>
using namespace std;
int Max(int a, int b){
return a>b ?a:b;
}
int FindGreatestSubarray(int *arr, int n){
int sum =arr[0];
int max =arr[0];
for(int i =1; i<n; i++){
sum =Max(sum+arr[i], arr[i]);
max =Max(sum, max)
}
return max;
}
int main()
{
return 0;
}
|
本题目的要求是从二位的数组中求解最大的子矩阵。我们可以将其转化成一维数组的问题。如果是二维数组可以压缩为一维数组(我当时也是不懂这里)。如果最大子矩阵和原矩阵等高,就可以这样压缩。
不是很懂,感觉K 的值应该是具有某种限制,但是这个仍然是 0-k 这样的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include<stdio.h>
#include<iostream>
#include<vector>
using namespace std;
#define inf 0x3f3f3f3f
int Max(int a, int b){
return a>b? a:b;
}
// 求解一维数组的最大连续子数列
int FindGreatestSubarray(int *arr, int n){
int sum =arr[0];
int max =arr[0];
for(int i =1;i<n;i++){
sum =Max(sum+arr[i], arr[i])
if(sum >=max){
max =sum;
}
}
return max;
}
int GreatestMatrix(int[][] arr, int rows, int cols){
int maxVal =- inf
for(int i =0 ; i <rows; i++){
vector<int> temp(arr[i]);
maxVal =Max(maxVal, FindGreatestSubarray(temp));
// 得到第一行的最大和
// 将行的n个元素加到上一行,然后计算最大和
for(int j =i+1; j<rows; j++){
for(int k =0;k<cols ;k++){
temp[k] =arr[j][k];
}
// 依次0~k行的最大和
maxVal =Max(maxVal, FindGreatestSubarray(temp))
}
}
}
int main(){
}
|
KMP(字符串高效查找)
计算部分匹配表
前缀和后缀的定义:“前缀"指除了最后一个字符以外,一个字符串的全部头部组合;“后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
如果给定的模式串是:“ABCDABD”,从左至右遍历整个模式串,其各个子串的前缀后缀分别如下表格所示:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
def kmp_match(s, p):
m, n =len(s) ,len(p)
cur =0
table = partial_table(p)
while cur <= m-n:
for i in range(n):
if s[i+cur] != p[i]:
cur += max(i -table[i-1], 1)
break
else:
return True
return False
def partial_table(p):
prefix =set()
postfix =set()
ret =[0]
for i in range(1, len(p)):
prefix.add(p[:i])
postfix ={ p[j:i+1] for j in range(1, i+1)}
ret.append(len((prefix & postfix or {''}).pop())) # &两个set求交集
return ret
print(partial_table('ABCDABD'))
print(kmp_match("BBC ABCDAB ABCDABCDABDE", "ABCDABD"))
|
kmp 算法的时间复杂度是 $O(m +n)$ 其中 m, n 分别表示pattern 和string 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include<iostream>
using namespace std;
const int N =1e4+11;
const int M =1e5+11;
int n, m;
char p[N], s[M];
int nex[N];
void get_next()
{
for(int i =2, j =0; i<=n ; i++)
{
while(j && p[i] != p[j +1]) j =nex[j];
if(p[i] ==p[j+1]) j ++;
nex[i] =j;
}
}
int main()
{
cin >>n >> p +1>> m>> s +1;
get_next();
// i 表示 s的遍历, j 表示p 的遍历
for(int i =1, j =0; i<=m; i++)
{
while(j && s[i] != p[j+1]) j =nex[j];
if(s[i] ==p[j+1]) j ++;
if(j ==n)
{
printf("%d ", i-n);
j =nex[j];
}
}
return 0;
}
|
二叉树的遍历
关于树的遍历,可以有先序,中序和后序遍历方式。有递归和非递归两种方式。所以总共有 6种实现方式。
在python中二叉树的结构:
1
2
3
4
5
|
class BinNode():
def __init__(self, val):
self.value =val
self.lchild =None
self.rchild =None
|
先序遍历(preOrder)
第一种思路是递归实现,第二种思路借助栈的结构来实现。栈的大小空间为O(h),h为二叉树高度;时间复杂度为O(n),n是树的节点的个数。
递归的写法便于理解,循环的方式内存比较省。
循环的版本从变量命名和结构上都是可以优化的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res, stack =[], [root]
while stack:
cur_node =stack.pop() # default pop(-1) 这个时间复杂度是 O(1),如果是pop(0) 那么时间复杂度是 O(n)
if cur_node:
res.append(cur_node.val)
stack.append(cur_node.right) # 注意这个顺序,这个是正确的姿态
stack.append(cur_node.left)
return res
|
c++ 递归版本
对于递归,应该先考虑是整个递归的过程主线,而不是跳出的条件(该问题比较细,然后很容易陷进去)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> res;
vector<int> preorderTraversal(TreeNode* root) {
if(!root) return res;
res.push_back(root-> val);
if(root -> left) preorderTraversal(root -> left);
if(root -> right) preorderTraversal(root -> right);
return res;
}
};
|
c++非递归版本,注意使用的是栈这种结构,并且在push() 的时候是先push(root-> right) 然后是 push(root -> left) 这样能够保证先弹出来 root ->left 结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 如果是非递归版本,使用的是栈 这种结构
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if(! root) return res;
stack<TreeNode *> s;
s.push(root);
while(s.size())
{
auto t =s.top();
s.pop();
res.push_back(t->val);
if(t ->right) s.push(t->right);
if(t->left) s.push(t->left);
}
return res;
}
};
|
中序遍历(inorder)
递归和非递归两种实现思路。入栈的顺序是一样的,只是改变的遍历(print())的顺序. 中序遍历是先把所有的左子树遍历完之后,然后遍历根节点,然后遍历右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
# 递归
def inOrder(self, root):
if root ==None:
return
self.inOrder(root.lchild)
print(root.val)
self.inOrder(root.rchild)
# 借助栈结构
class Solution:
def inorderTraversal(self, root):
res, stack =[], []
while True:
while root:
stack.append(root)
root =root.left
if not stack:
return res
node =stack.pop()
res.append(node.val)
root =node.right
|
c++ 中序遍历递归写法, 中序遍历是先一直遍历到子树的最左边,然后回溯遍历根节点,然后遍历右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 使用中序遍历,dfs
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
if(! root) return res;
if(root -> left) inorderTraversal(root ->left);
res.push_back(root -> val);
if(root -> right) inorderTraversal(root ->right);
return res;
}
};
|
c++ iteration 版本,使用一个栈来模拟过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode *> s;
TreeNode* p =root;
while(p || s.size())
{
// bad case 如果最开始的时候, 根节点的左孩子是空,那么就没有放进去
while(p)
{
s.push(p);
p =p->left;
}
auto t =s.top();
s.pop();
res.push_back(t->val);
if(t-> right) p=t->right;
}
return res;
}
};
|
后序遍历(post order)
仍然是递归和非递归版本,非递归中使用两个stack,两个stack的后进先出等于一个先进先出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
# 递归
def postOrder(self, root):
if root == None:
return
self.postOrder(root.lchild)
self.postOrder(root.rchild)
print(root.val)
# 借助栈结构
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def postorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res, stack =[], [root]
while stack:
cur_node =stack.pop()
if cur_node:
res.append(cur_node.val)
stack.append(cur_node.left) # 注意和先序遍历的顺序,还有最后的 reverse 操作
stack.append(cur_node.right)
return res[::-1]
|
c++ 后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 递归写法
vector<int> res;
vector<int> postorderTraversal(TreeNode* root) {
if(! root) return res;
if(root -> left) postorderTraversal(root -> left);
if(root -> right) postorderTraversal(root -> right);
res.push_back(root -> val);
return res;
}
};
|
依赖于前序遍历而实现的后序遍历, cpp 迭代版本。最后使用 reverse 函数实现vector 的反转。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 如果是前序可以使用 栈模拟,那么后序同样是可以使用栈来模拟的
vector<int> res;
vector<int> postorderTraversal(TreeNode* root) {
if(!root ) return res;
// 因为是后进先出,所以先要把跟结点放到stack 中
stack<TreeNode *> s;
auto p =root;
s.push(p);
while(s.size())
{
auto t =s.top();
s.pop();
res.push_back(t->val);
if(t-> left) s.push(t->left);
if(t-> right) s.push(t->right);
}
reverse(res.begin(), res.end());
return res;
}
};
|
层序遍历
使用到了队列的思想,先进先出。实际上,用的是Python中list.pop(0).注意默认是list.pop(-1),也就是默认弹出的是最后一个元素。
层序遍历使用 while 循环就比较好理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
def levelOrder(self, root):
if root ==None:
return
myQueue =[]
node =root
myQueue.append(node)
while myQueue:
# remove and return item at index (default last)
node =myQueue.pop(0)
print(node.val)
if node.lchild != None:
myQueue.append(node.lchild)
if node.rchild != None:
myQueue.append(node.rchild)
|
旋转数组找最小值
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
直接是二分的思路,时间复杂度是 $O(logn)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
// 这里说 no duplicates,所以不用处理一个条件
// 比较 nums[0] 和 nums[mid] 关系, if nums[mid] > nums[0] l = mid +1
int findMin(vector<int>& nums) {
int n = nums.size();
if(n ==1) return nums[0];
if(nums[0] < nums[n-1]) return nums[0];
int l =0, r =n -1;
while(l < r)
{
int mid =l +r >>1;
// 如果 mid 和0 表示一个位置,那么该解也不是最小值,虽然没有重复的元素,但这个等于号是应该在这里的
if(nums[mid] >= nums[0]) l =mid +1;
else
r =mid ;
}
return nums[l];
}
};
|
c++ 版本 循环法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
// 对于链表操作修改的list,需要使用到三个指针, pre, cur, next 所以空间复杂度是 O(1), 空间复杂度是 $O(n)$
ListNode* reverseList(ListNode* head) {
ListNode * pre =nullptr;
ListNode * cur = head;
while(cur)
{
ListNode * next =cur ->next;
cur ->next = pre;
pre =cur, cur = next;
}
return pre;
}
};
|
python 版本 ,迭代版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre =None
cur =head
while cur:
nex =cur.next
cur.next = pre
pre =cur
cur =nex
return pre
|
还可以使用递归的思路进行求解,具体参考这里, 遍历所有的结点,时间复杂度是 $O(n)$, 需要 $n$ 个栈空间,空间复杂度是$O(n)$。
Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).
1
2
|
Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"
|
c++ 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
// 首先对于 t 进行 hash, 然后再s 中使用双指针 i j , i >=j ,时间复杂度是 $O(n)$
// 空间是 $O(n)$
string minWindow(string s, string t) {
unordered_map<char, int> hash;
int cnt =0; // unique character
for(auto ch : t)
{
if(!hash[ch]) cnt ++;
hash[ch] ++;
}
string res ="";
for(int i=0, j =0, c =0; i< s.size(); i ++)
{
// 往里面加
if(hash[s[i]] == 1) c ++;
hash[s[i]] --;
while(c ==cnt && hash[s[j]] <0) hash[s[j++]] ++;
if(c ==cnt)
{
if(res.empty() || res.size() > i-j +1) res =s.substr(j, i -j +1);
}
}
return res;
}
};
|
python 实现,也是双指针 + dictionary, 和上面的c++ 代码中有的变量名表示的含义不同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution(object):
def minWindow(self, s, t):
"""
:type s: str
:type t: str
:rtype: str
"""
from collections import Counter
dic , cnt =Counter(t), len(t)
i , start, end =0, 0, 0
# muberate(string, start_index) 从1 开始计数
for j, ch in enumerate(s, 1):
cnt -= dic[ch] >0
dic[ch] -=1
if not cnt:
while dic[s[i]] <0:
dic[s[i]] += 1
i +=1
if end ==0 or j -i < end -start:
start, end =i, j
dic[s[i]] +=1
i +=1
cnt +=1
return s[start: end]
|




