之前在介绍宽度优先遍历、深度优先遍历、拓扑排序、最小生成树、并查集的时候零零散散介绍过图，这篇以图为中心，介绍相关的算法。

定义和表示

（1）定义

An undirected graph is connected if every pair of vertices is connected by a path.

A forest is an acyclic graph, and a tree is a connected acyclic graph. A graph that has weights associated with each edge is called a weighted graph. 从图的角度解读树。

统一符号，$V$（vertex）表示顶点，$E$（edge）表示边（权重）。

（2）邻接表表示

The adjacency list representation of a graph G = (V, E) consists of an array $Adj_{[1..|V |]} $ of lists. Each list $Adj_{[v]} $is a list of all vertices adjacent to v.

（3）邻接矩阵表示

Adjacency matrices have a value $a_{i,j} = 1 $ if nodes i and j share an edge; 0 otherwise. In case of a weighted graph, $a_{i,j} = w_{i,j} $, the weight of the edge. 通过0和1 标识是否存在边；是对称矩阵，可以只存储上三角形和下三角形。

（4）分类

对于图来说，根据有无权重可以分为两类；根据是否有方向可以分为两类；根据是否有环，可以分成两类；根据点和边的个数相对大小，可以分为稠密图和稀疏图；并且这种是可以线性组合的，比如说有向无权重，有向有权重。

图的遍历算法

Graph Search Algorithms

宽度优先算法

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a search key), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level. 宽度优先（Breadth-First Search）是图或者树的一种遍历算法。宽度优先算法从树或者图的某一点出发，首先遍历当前节点周围邻居节点，然后进入下一层的遍历。这种遍历的思想和队列非常相像，所以在BFS 中经常出现队列的数据结构。

深度优先算法

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. 深度优先算法（Depth-First Search）选择一个根节点（或者随意一个起点）然后沿着一条路径尽可能走下去，当走不通的时候就回溯。这种思想和栈非常类似。

最小生成树

A spanning tree of an undirected graph G is a subgraph of G that is a tree containing all the vertices of G. 生成树的定义：包含所有节点且包含部分边的图。

A minimum spanning tree (MST) for a weighted undirected graph is a spanning tree with minimum weight. 最小生成树的定义：在有权重的图中，图权重为所有边权重之后，那么最小生成树就是所以生成树中权重和最小大的。

Prim Algorithm

In computer science, Prim’s (also known as Jarník’s) algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex. 基于贪心的策略。从任意一点开始，每次迭代选择的是点（最小的边是附带产物），适合在稠密图中使用。时间复杂度$O(V^2 +E)$，其中$V$表示点的个数， $E$表示边的个数。

A demo for Prim’s algorithm based on Euclidean distance.

图中所示，给定一个起点（任意一个起点），然后选择距离该点距离最近（这里是欧式距离）点，加入到现有的点的集合中，以此类推，直到有$E-1$条边或者连接了所有的点。

Prim算法求最小生成树

时间复杂度是 $O(V^3)$， 其中 $V$表示点的个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N =510, INF =0x3f3f3f3f;
int n, m;
int g[N][N];

int dist[N];
bool st[N];

int prim(){
    memset(dist, 0x3f, sizeof dist);
    int res =0;
    for(int i =0; i< n; i++)
    {
        int t =-1;
        // 选择权重最小的边
        for (int j =1; j<=n; j++)
        {
            if(!st[j] && (t ==-1 || dist[t] > dist[j]))
                t =j;
        }
        if(i && dist[t] ==INF) return INF;
        if(i) res += dist[t];
        
        for(int j =1; j<=n; j++)
            dist[j] =min(dist[j], g[t][j]);
        st[t] =true;
    }
    return res;
}

int main()
{
    cin >> n>>m;
    memset(g, 0x3f, sizeof g);
    while(m --)
    {
        int a, b,c;
        cin >>a>>b>>c;
        g[a][b] =g[b][a] =min(g[a][b], c);
        
    }
    int t =prim();
    if(t ==INF) cout << "impossible" << endl;
    else cout << t << endl;
    return 0;
}

Kruskal Algorithm

基于贪心的策略。从权重最小的边开始，每次迭代选择的是边（点是附带的产物），适合在稀疏图中使用。时间复杂度$ElogE$，其中 $E$表示边的个数， $V$表示点的个数（虽然没有用到）。算法步骤（A demo for Kruskal algorithm based on Euclidean distance.）：

KruskalDemo.gif 图中所示，每次选择是距离最短的边（顺便把点连接起来），在这过程中需要判断是否形成了环（如果是回溯），直到连接了所有的点或者是$V-1$条边。

Kruskal算法求最小生成树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

#include<iostream>
#include<algorithm>
using namespace std;
const int N =1e5+11, M =2e5+11, INF =0x3f3f3f3f;
int n, m;
int p[N];

struct Edge
{
    int a, b, w;
}edges[M];
int find(int x)
{
    // 这个是递归的定义，只需要一次if 就行，不要使用 while
    if(p[x] != x) p[x] =find(p[x ]);
    return p[x];
}
bool cmp(Edge a,  Edge b)
{
    return a.w< b.w;
}
int kruskal()
{
    sort(edges, edges +m, cmp);
    for(int i =1; i<=n; i++) p[i] =i;
    int res =0, cnt =0;
    for(int i =0; i<m ;i++)
    {
        int a =edges[i].a, b =edges[i].b, w =edges[i].w;
        a =find(a), b =find(b);
        if(a !=b)
        {
            p[a]=b;
            res +=w;
            cnt ++;
        }
    }
    if (cnt !=n -1) return INF;
    return res;
}
int main()
{
    cin >> n>>m;
    for(int i =0; i<m; i++)
    {
        int a, b, w;
        cin >>a>>b>>w;
        edges[i] ={a, b, w};
    }
    
    int t =kruskal();
    
    if(t ==INF) puts("impossible");
    else cout<<t<<endl;
}

最短路径

最短路径的常用算法有迪杰克斯拉算法（Dijkstra Algorithm），贝尔曼福特算法（Bellman-Ford Algorithm）和弗洛伊德算法（Floyd-Warshall Algorithm）。相同点：三个算法的核心思想：边$(u, v)$是从结点$u$到结点$v$， 如果 $dist(v) > dist(u) + w(u, v)$，那么 dist(v) 就可以被更新。不同点：其中Floyd 算法是多源最短路径，即求解任意点到任意点的最短路径，而Dijkstra 算法和Bellman-Ford Algorithm 是求解单源最短路径，即单个点到任一点的最短路径。其中Dijkstra算法要求权值全部为正，其他的两种可以处理负权边，但是不能出现负环（所谓的负环，就是权值总和为负的环）。

Dijkstra’s Algorithm

单源最短路径算法（Single-Source Shortest Paths）的特点：

  • Dijkstra 是起点到终点（其他所有点）的最短路径（单源）
  • 要求权值非负
  • 堆优化之后时间复杂度 $O(Elog V)$， $E$表示边数，$V$ 表示点数；普通的算法时间是 $O(V^2 + E)$
  • 如果想要得到所有点的最短路径，那么需要在 $V$个点上执行相同的操作，总的时间复杂度是 $O(V^3)$

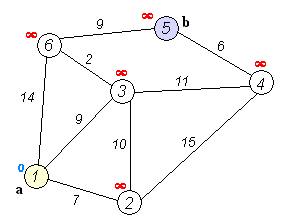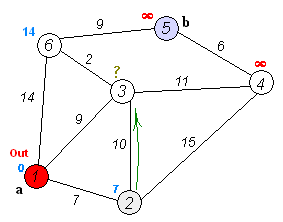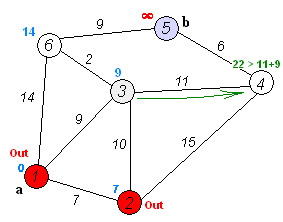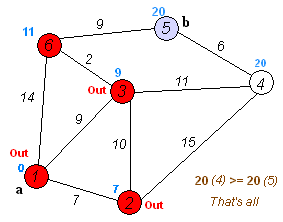
算法步骤示意图： Dijkstra_Animation.gif

（1） Network Delay Time

时间复杂度是$O(E +VlogV)$, 空间复杂度是$O(V+E)$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import heapq
class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        graph=collections.defaultdict(dict)
        for source, dest, cost in times:
            graph[source][dest]  =cost
        distances ={i : float('inf') for i in range(1, N+1)}
        distances[K] =0
        min_heap=[(0, K)]
        visited =set()
        while min_heap:
            dis, vec = heapq.heappop(min_heap)
            if vec in visited: continue
            visited.add(vec)
            for neighbor in graph[vec]:
                if neighbor in visited: continue
                new_dis =dis + graph[vec][neighbor]
                if new_dis < distances[neighbor]:
                    distances[neighbor] =new_dis
                    heapq.heappush(min_heap, (new_dis, neighbor))
        if len(visited) != len(distances): return -1
        return max(distances.values())

（2）Cheapest Flights Within K Stops

多关键字的最短路径问题，时间复杂度是$O(E + Vlog KE)$，其中 $E$表示边的个数， $V$表示点的个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        graph =collections.defaultdict(list)
        
        for beg, end, w in flights:
            graph[beg].append([w, end])
        min_heap =[[0, src, 0]] # 如果是小根堆，那么使用python实现，大根堆使用c++ 实现
        while min_heap:
            w, beg , stops =heapq.heappop(min_heap)
            if beg == dst:
                return w
            if stops > K:
                continue
            for  nex_w, nex_dst in graph[beg]:
                heapq.heappush(min_heap, [w + nex_w, nex_dst, stops +1])
        return -1

Bellmann-Ford Algorithm

The basic idea of SPFA is the same as Bellman–Ford algorithm in that each vertex is used as a candidate to relax its adjacent vertices. The improvement over the latter is that instead of trying all vertices blindly, SPFA maintains a queue of candidate vertices and adds a vertex to the queue only if that vertex is relaxed. This process repeats until no more vertex can be relaxed. Bellmann-Ford Algorithm (SPFA，Shortest Path Faster Algorithm)用于处理有环且含有负权重的加权有向图。基本的原理是对图进行 V-1次松弛操作，得到所有可能的最短路径。

Bellmann-Ford Algorithm的特点：

  • 用于求含有负权边的最小生成树或者判断负权环
  • 队列优化之后，平均时间 $O(E)$，最坏的情况下是 $O(EV)$，其中 $E$表示边数， $V$表示点数

A demo of SPFA based on Euclidean distance. Red lines are the shortest path covering (so far observed). Blue lines indicate where relaxing happens, i.e., connecting $v$ with a node $u \in Q$, which gives a shorter path from the source to $v$.

（1） Network Delay Time

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        arr =[float('inf')] *N
        arr[K-1] =0
        update =True
        
        while update:
            update =False
            for e in times:
                x, y , w =e[0] -1, e[1] -1, e[2]
                if arr[x] < float('inf') and arr[y] > arr[x] +w:
                        arr[y] =arr[x] +w
                        update =True
        return max(arr) if max(arr) < float('inf') else -1

Floyd 算法

In computer science, the Floyd–Warshall algorithm (also known as Floyd’s algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm) is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles).

The Floyd–Warshall algorithm is an example of dynamic programming

A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm.

  • Floyd 算法是任意两点之间的最短路径（多源）
  • 权值可以为负数，不能有负数的环
  • 时间复杂是$O(V^3)$， $V$表示点的个数

（1） Network Delay Time

时间复杂度是 $O(V^3)$， 空间是 $O(V^2)$。Floyd相对于 Dijkstra 算法是比较简单，但是时间复杂度是比较高。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        dist = [[float('inf') for _ in range(N)] for _ in range(N) ]
        for u, v, w in times:
            dist[u-1][v-1] =w
        for i in range(N):
            dist[i][i] =0
        
        for k in range(N):
            for i in range(N):
                for j in range(N):
                    dist[i][j] =min(dist[i][j], dist[i][k] + dist[k][j])
        return max(dist[K-1]) if max(dist[K-1]) < float('inf') else -1

拓扑排序

见Breadth First Search 中有向图小结。

连通性

拓扑排序

判断是否有环（无环图的所有点都是可以进行拓扑排序）

并查集

Redundant Connection

时间复杂度是$O(n)$， 讲解。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
public:
    vector<int> p;
    void init(int n)
    {
        for(int i =0; i< n; i++)
            p.push_back(i);
    }
    int find(int x)
    {
        if(x != p[x]) p[x] =find(p[x]);
        return p[x];
    }
    bool is_union(int x, int y)
    {
        int t1 =find(x);
        int t2 =find(y);
        if( t1 ==t2) return true;
        else
        {
            p[t1] =p[t2];
            return false;
        }
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n =edges.size() ;
        init(n+1);
        vector<int> res(2, 0);
        for(int i =0; i< n; i++)
        {
            int x =edges[i][0];
            int y =edges[i][1];
            if(is_union(x, y))
            {
                res[0] =x;
                res[1] =y;
            }
        }
        return res;
    }
};

并查集讲解

参考文献

Wikipedia Leetcode