贪心算法,分为定义,使用条件,不足之处和常见例题(代码)等部分。
概念
(1)定义
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage with the intent of finding a global optimum.
贪心算法根据当前一步的局部最优解来求解最后的全局最优解。所谓启发式(heuristic)是在可接受的代价(计算时间和空间)条件下,给出一个可行解,可行解和最优解偏离程度无法保证,计算时间无法保证。
(2)使用条件
1). 贪心选择性质(Greedy choice property)
A global (overall) optimal solution can be reached by choosing the optimal choice at each step.(hard to prove its correctness!). If you make a choice that seems the best at the moment and solve the remaining sub-problems later, you still reach an optimal solution. You will never have to reconsider your earlier choices.
在每一步都是计算最优解,不需要考虑之前的决策,最优解可以局部最优解获得。(很难去证明)
2). 最优子结构(optimal substructure)
A problem has an optimal substructure if an optimal solution to the entire problem contains the optimal solutions to the sub-problems.
全局的最优解包含子问题的最优解。比如说在起点$P_s$到终点$P_e$的全局最优路径包含中间某点 $P_m$到终点 $P_e$的最优路径。
(3)贪心算法和动态规划算法的异同
1). 都满足最优子结构的性质
2). 全局最优解可以通过局部最优解得到 是和动态规划的主要区别。动态规划是自底向上,而贪心算法通常是自顶向下求解。
(4)优缺点
优点:一个算法问题使用暴力解可能需要指数级别的时间;使用动态规划思想消除重复的子问题,可以达到多项式级别的复杂度;如果满足贪心选择性质,可以进一步降低到线性级别的复杂度。所以如果能使用贪心,那么时间复杂度是比较小的。
缺点:
Sometimes greedy algorithms fail to find the globally optimal solution because they do not consider all the data. The choice made by a greedy algorithm may depend on choices it has made so far, but it is not aware of future choices it could make.
例题(代码)
(1)Fractional Knapsack problem(分数,小数背包问题)
问题描述:给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包的容量为C 应如何选择装入背包的物品 使得装入背包中物品的总价值最大? 这里,在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,不能重复装载。(物品可以任意切分)
(如果问题不可分,那么应该参考动态规划中的01 背包问题)
(2)区间调度问题(Interval Scheduling)
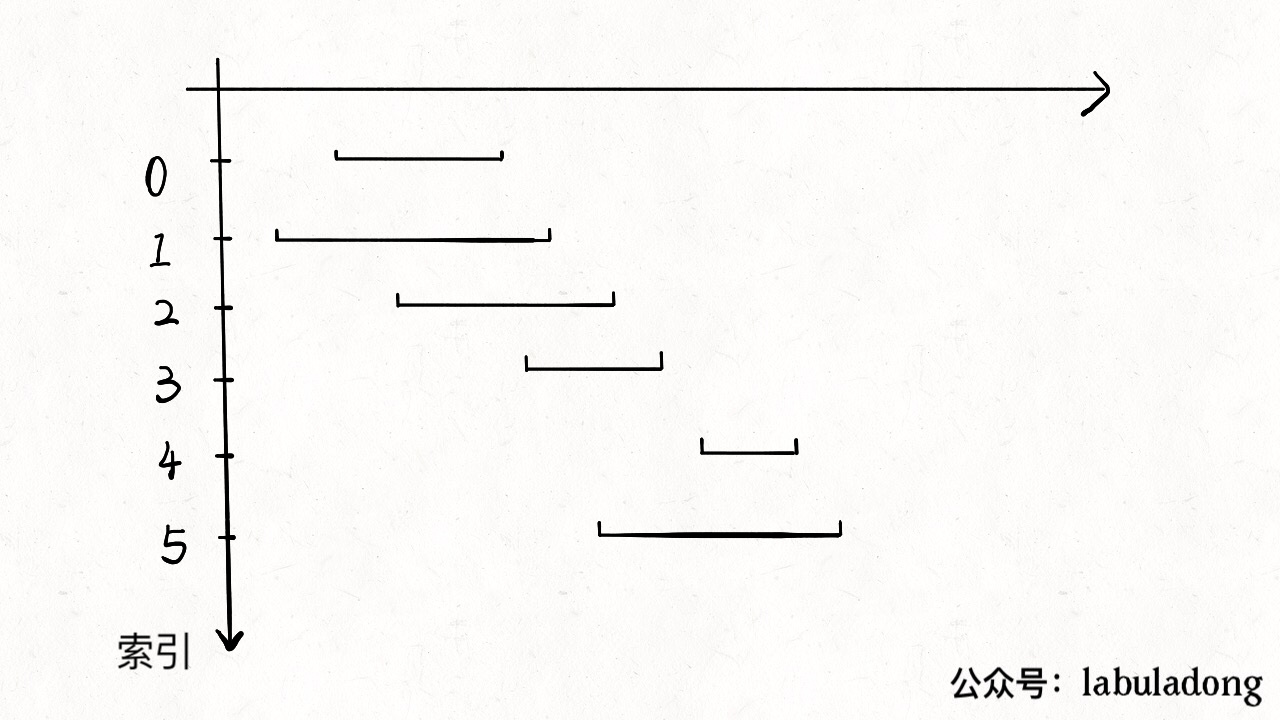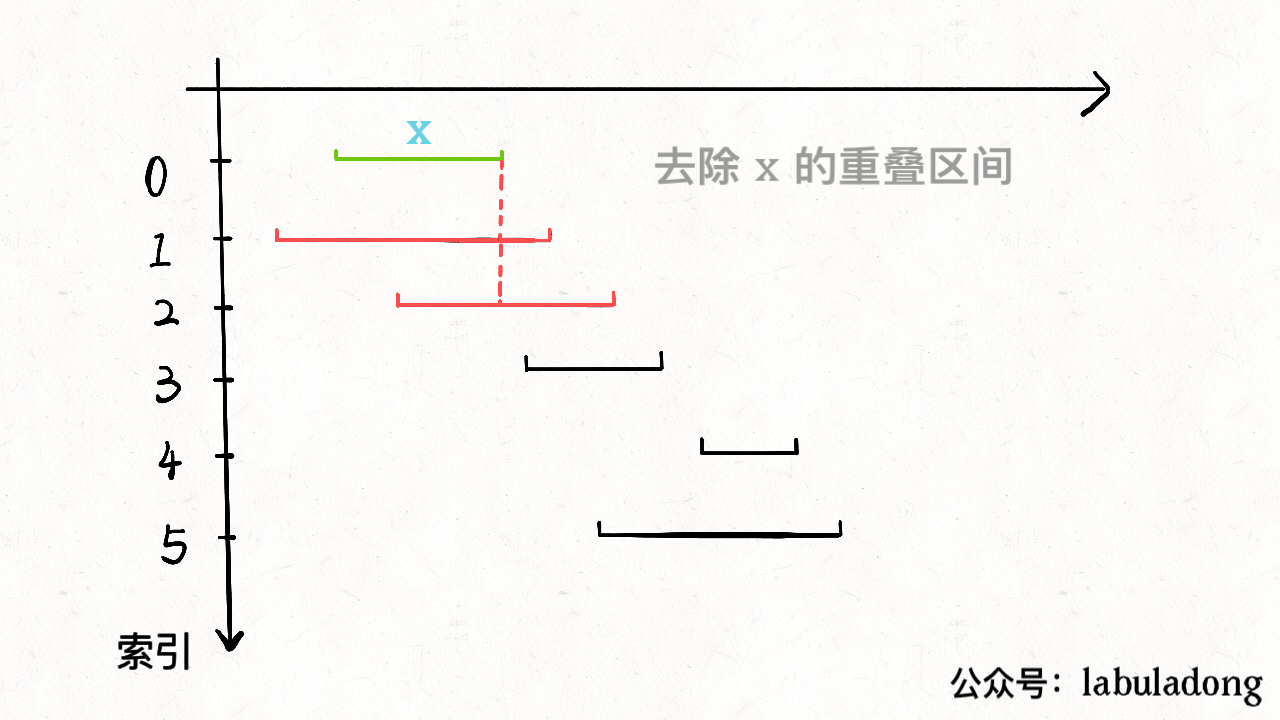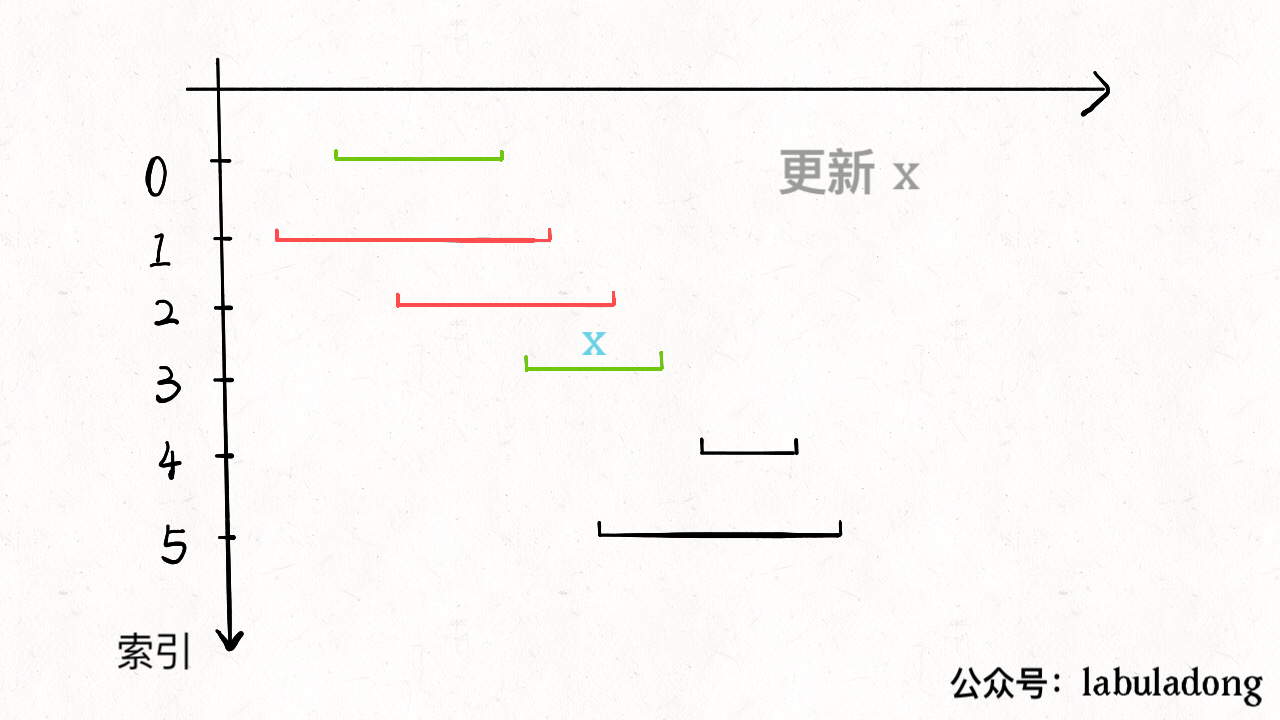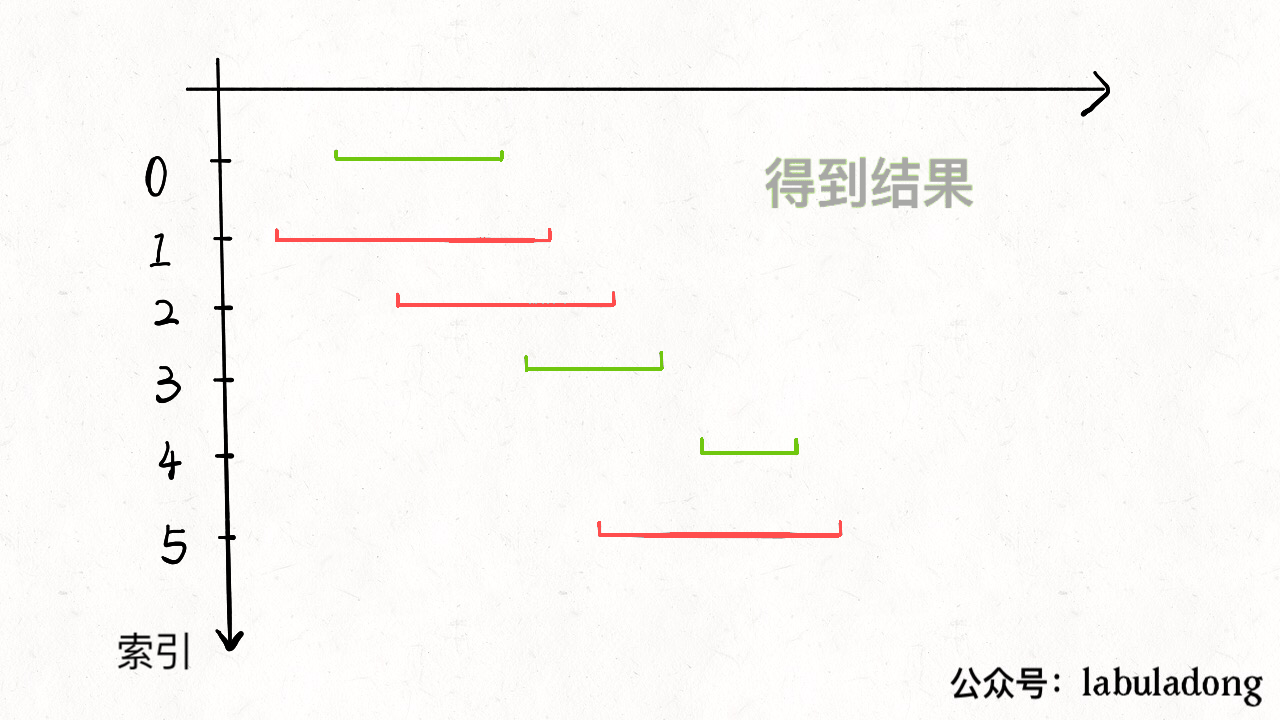
1). Non-overlapping Intervals
找到不会重叠的区间,那么剩下的就是需要去除的区间。下图更加形象说明这一过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
static bool cmp(vector<int> &x, vector<int> &y)
{
return x[1] < y[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.empty()) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int ans =1;
int right =intervals[0][1];
for(int i =1; i< intervals.size(); i++)
{
if(right <= intervals[i][0])
{
ans +=1;
right =intervals[i][1];
}
}
return intervals.size() -ans;
}
};
|
c++语法
1
2
3
|
对于双元素(pair or 结构体),默认是先按照第一个元素增序排列,然后按照第二个元素增序排列;如果是自定义排序方法,那么就是按照第二个元素排序,第一个元素是无序的。
static 静态修饰 cmp 函数
|
python代码实现。
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals: return 0
# 贪心算法
intervals.sort(key =lambda x: x[1]);
counts =1
right =intervals[0][1]
for i in range( len(intervals)):
if(right <= intervals[i][0]):
counts +=1
right =intervals[i][1]
return len(intervals) -counts
|
2). 活动安排的题目
c++ 实现。贪心算法
贪心算法+ 大根堆,
思路和区间问题差不多
按照结束时间排序,统计一个总的时长,如果总时长没有超过 结束时间,那么就可以加到里面;否则弹出耗时最长的那个
c++ 中默认是大根堆, python 中默认是小根堆;因为c++ 是比较大的,所以大根堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
static bool cmp(vector<int> &a, vector<int> &b)
{
return a[1]< b[1];
}
int scheduleCourse(vector<vector<int>>& courses) {
priority_queue<int> max_heap;
sort(courses.begin() , courses.end(), cmp);
int t2n = 0; // time to noew
for(int i =0; i< courses.size(); i++)
{
if(t2n +courses[i][0] <= courses[i][1])
{
max_heap.push(courses[i][0]);
t2n += courses[i][0];
}
else if(!max_heap.empty())
{
if(max_heap.top() > courses[i][0])
{
t2n = t2n -max_heap.top() +courses[i][0];
max_heap.pop();
max_heap.push(courses[i][0]);
}
}
}
return max_heap.size();
}
};
|
python中使用 heapq.heappush() 和heapq.heappop() 两个方法构建小根堆的push 和pop 操作,需要另外申请一个list。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution:
def scheduleCourse(self, courses: List[List[int]]) -> int:
# 使用大根堆保存时长,按照结束时间进行排序(时间安排类问题常见的做法)
courses.sort(key =lambda x: x[1])
# python 中使用 heapq.heappush() heapq.heappop() 来构建大根堆和小根堆
t2n =0
min_heap =[]
for t, d in courses:
heapq.heappush(min_heap, -t)
t2n += t
if t2n >d:
t2n += heapq.heappop(min_heap)
return len(min_heap)
|
(2)旅行商问题( Travelling Salesman )
The travelling salesman problem (also called the travelling salesperson problem[1] or TSP) asks the following question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?” It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.
给定若干个城市和每个城市之间的距离,寻找一条最短可能的路径使得遍历每个城市,并且回到原先出发的城市。这是一个NP 问题,意味着无法在多项式的时间内解决,随着城市个数的增加,排雷组合的方式增长(阶乘,非指数)。目前其中一种解决方案是基于启发式的方式,贪心。
(3)best time to buy and sell stock
1). best-time-to-buy-and-sell-stock
贪心,基于当前计算profit 和买入点;然后遍历全部。最多进行一次交易(买入一次,卖出一次)。在初始化的使用 buy= prices[0],因为第一个元素只可能买入,不可能卖出。剩下部分是$O(n)$ 的时间遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
if(prices.empty()) return prices;
// 贪心,选择当前最优的;遍历一遍更新
int profit =0, buy =prices[0];
for(int i =1; i< prices.size(); i++)
{
profit =max(profit, prices[i]- buy);
buy =min(buy, prices[i]);
}
return profit;
}
};
|
python版本
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if not prices: return 0
buy =prices[0]
profit =0
for i in range(1, len(prices)):
profit =max(profit, prices[i] -buy)
buy =min(buy, prices[i])
return profit
|
2). Best Time to Buy and Sell Stock II
第二版本是能够买卖无限次。还是使用贪心的思想。只有是当前价格大于前一天的价格,那么就买入。(贪心算法,类似寻找增序列)。使用贪心比较好理解一些。
c++ 版本
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n =prices.size();
int profit =0;
for(int i =1; i< n; i++)
{
profit += prices[i] > prices[i-1] ? prices[i] -prices[i-1] : 0;
}
return profit;
}
};
|
python 版本
1
2
3
4
5
6
7
8
9
10
11
|
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if not prices: return 0
profit =0;
for i in range(1, len(prices)):
profit += prices[i] -prices[i-1] if prices[i] > prices[i-1] else 0
return profit
|
解法二:动态规划
- 状态表示 $f(i)$ 表示第$i$ 天,不持有股票的最大收益, $g(i)$ 表示第$i$ 天,持有股票的最大收益
- 转移方程, $f(i)$第 $i$天不持有股票,有两种可能性:前一天不持有股票或者前一天持有并且当天卖出,两者取最大值;$g(i)$第$i$天持有股票,有两种可能性:前一天持有股票或者前一天不持有股票当天买入,然后两者取最大值。数学表达为
$$
\begin{split}
f(i) &= max(f(i-1), g(i-1) + prices[i]) \\
g(i) &= max(g(i-1), f(i-1) -prices[i])
\end{split}\tag{1.3}
$$
- 初始化, $f(0) =0$, $g(0)=-\infty $
时间复杂度 $O(n)$,空间复杂度度可以优化为 $O(1)$。所以就本题而言,从时间和空间复杂度分析,贪心算法足以。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
// 这个不是 easy 难度,感觉至少是 medium 难度
// 使用两个函数表示, f 表示不持有, g 表示持有
int maxProfit(vector<int>& prices) {
int n = prices.size();
int last_f, f=0 , last_g, g= -100000; // g 的初始化注意
for(int i =0; i < n; i++)
{
last_f =f;
last_g =g;
f = max(last_f, last_g + prices[i]);
g = max(last_g, last_f -prices[i]);
}
return f; // 最后是卖了,不持有
}
};
|
3). Best Time to Buy and Sell Stock III
限制条件最多进行两次交易。两种思路:动态规划 和贪心。动态规划:两次遍历,第一次从左到右,找出一次购买的最大值;第二次从右到左,找出第二次购买的最大值。$ f[i] $表示前i 的最大利润,$ f[i] =max(f[i-1], prices[i] -minv[i-1])$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n =prices.size();
if(!n) return 0;
vector<int> f(n, 0);
int minv =INT_MAX;
for(int i =0; i<n; i++ )
{
if(i) f[i] =f[i-1];
if(prices[i] >minv )
{
f[i] =max(f[i], prices[i] -minv);
}
minv =min(minv, prices[i]);
}
int maxv =INT_MIN;
int res =f[n-1];
for(int i =n-1; i>0; i--)
{
if(prices[i] < maxv)
{
res =max(res, maxv-prices[i]+ f[i-1]);
}
maxv =max(maxv, prices[i]);
}
return res;
}
};
|
python实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 两次遍历 , f[i] 表示前 i天的最大的收益; 计算方法就是股票- 最小值
if not prices: return 0
n =len(prices)
f =[0] *n
minv = prices[0]
for i in range(n):
if(i): f[i] =f[i-1]
if(prices[i] > minv) :
f[i] =max(f[i], prices[i] -minv)
minv =min(minv, prices[i])
# 第二次
res = f[n-1]
maxv =prices[n-1]
for i in range(n-1 ,0, -1 ):
if(prices[i] < maxv):
res =max(res, maxv- prices[i] + f[i-1])
maxv =max(maxv, prices[i])
return res
|
贪心(暴力)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
one_buy = two_buy = sys.maxsize
one_profit = two_profit = 0
for p in prices:
one_buy = min(one_buy, p)
one_profit = max(one_profit, p - one_buy)
two_buy = min(two_buy, p - one_profit) # 为什么和 one_profit 进行比较呢
two_profit = max(two_profit, p - two_buy)
return two_profit
|
4). Best Time to Buy and Sell Stock IV
动态规划的思想
- 定义dp状态dp[i][j] 表示第j 天,第i笔交易产生的最大的收益
- 转移方程 dp[i][j] =max(dp[i][j-1], tmp +prices[j] ) 处理卖出的情况
- tmp 表示已经获得的最大的利润, 处理的是买入的情况
如果买卖的次数$k \ge \frac{n}{2}$,那么就如同第二个题目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution(object):
def maxProfit(self, k, prices):
# tmp=max(tmp, dp[i-1][j-1]-prices[j] ) # 买入
# 初始化 dp[i][j] ={0}, tmp = -prices[i]
if k >= len(prices )>> 1: return self.maxProfit2(prices)
dp =[ [0] *(len(prices)) for _ in range(k+1)]
for i in range(1, k+1):
tmp =-prices[0]
for j in range(1, len(prices)):
dp[i][j] =max(dp[i][j-1], tmp + prices[j])
tmp =max(tmp, dp[i-1][j -1] -prices[j])
return dp[k][-1]
def maxProfit2(self, prices):
res =0
for i in range(1, len(prices)):
if(prices[i] > prices[i-1]):
res += prices[i] -prices[i-1]
return res
|
第二种解法:分析时间复杂度和 $k$ 相关
1
2
3
4
5
6
7
8
9
|
def maxProfit(k, prices):
if k > len(prices) >> 1:
return sum(prices[i+1]-prices[i] for i in range(len(prices)-1) if prices[i+1]>prices[i])
cash, asset = [float('-inf')] * (k+1), [0] * (k+1)
for price in prices:
for i in range(1,k+1):
cash[i] = max(cash[i], asset[i-1]-price)
asset[i] = max(asset[i], cash[i]+price)
return asset[k]
|
(4)钱币找零
(这两道题目应该归结到动态规划中)
题目大意如下,对于人民币的面值有1元 5元 10元 20元 50元 100元,下面要求设计一个程序,输入找零的钱,输出找钱方案中最少张数的方案,比如123元,最少是1张100的,1张20的,3张1元的,一共5张!
1). Coin Change
完全背包问题,$f[j]$表示价值为$j$ 的所需的最少的数量,有如下的转移方程:$f[j] =min(f[j], f[j -coins[i]]+1)$。dp 关键是填表格,找到转移方程。
c++ 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int INF=10000000;
vector<int> f(amount+1, INF);
f[0] =0;
for(int i =0; i< coins.size() ; i++)
{
for(int j =coins[i]; j<= amount; j++)
{
f[j] =min(f[j], f[j -coins[i]]+1);
}
}
if(f[amount] ==INF) f[amount] =-1;
return f[amount];
}
};
|
python 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
# 使用dp的思想去做,关键是在于转移方程,填写二维或者三维表格的问题
# python中float('inf')表示无穷大
f=[float('inf')]*(amount +1)
f[0] =0
for coin in coins:
for i in range(coin, amount+1):
f[i] =min(f[i], f[i -coin] +1)
if(f[amount] ==float('inf')): f[amount] =-1
return f[amount]
|
float('inf')表示浮点数的最大值, float('-inf')表示浮点数的最小值。sys.maxsize 表示int 的最大值, -sys.maxsize-1 表示int 的最小值。
2). Coin Change 2
上一道题目求解的是能否问题,这一道题求解的是组合,共有多少种凑齐的方式。上面求解的是数量最少的一种方案。这里求解的是总共的方案。
C++ 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> f(amount+1, 0);
f[0] =1;
for(int i =0; i< coins.size(); i++)
{
for(int j =coins[i] ; j<=amount ; j++)
{
f[j] += f[j-coins[i]];
}
}
return f[amount];
}
};
|
python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution(object):
def change(self, amount, coins):
"""
:type amount: int
:type coins: List[int]
:rtype: int
"""
f =[0] *(amount +1)
f[0] =1
for coin in coins:
for i in range(coin, amount+1):
f[i] = f[i] + f[i-coin]
return f[amount]
|
(5) Largest Number
设有N个正整数,现在需要你设计一个程序,使他们连接在一起成为最大的数字,例3个整数 12,456,342 很明显是45634212为最大,4个整数 342,45,7,98显然为98745342最大程序要求:输入整数N 接下来一行输入N个数字,最后一行输出最大的那个数字!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
// 使用nlogn的算法,先进行排序
static bool cmp(int a, int b)
{
string sa =to_string(a), sb =to_string(b);
return sa+sb >sb +sa; // 这个保证是降序
}
string largestNumber(vector<int>& nums) {
sort(nums.begin(), nums.end(), cmp);
string res ="";
for(auto num : nums)
res += to_string(num);
for(int i =0; i< res.length(); i++)
if(i ==res.length() -1 || res[i] !='0')
return res.substr(i, res.length() -i); // 第二个参数是长度
return res;
}
};
|
c++语法,使用它 to_string() 和 substr(start, length) 两个很好用的字符串函数。
python 实现
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def largestNumber(self, nums):
"""
:type nums: List[int]
:rtype: str
"""
nums =map(str, nums)
nums.sort(cmp =lambda a, b : cmp(a+b, b+a), reverse= True)
return ''.join(nums).lstrip('0') or '0'
|
sort() 内置的cmp自定义函数是在python2 中使用的,在python3 中 from functools import cmp_to_key 进行自定义比较函数。
python中默认是升序 reverse =False, 但是这里需要 reverse =True 转换成降序
cmp(x, y), return 1 if x >y; return 0, if x ==y ; return -1 , if x< y
(6)最小生成树
1). Prim’s algorithm
Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
prim 是一种贪心算法,无向有权图中寻找最短生成树的算法。这意味着选定了图中边的子集,这些边集包含了所有的顶点,并且边集的权重是最小。算法步骤如下
- 将边集合按照权重升序排列
- 选择最小权重边对应的点,判断是否构成了环,如果是,那么忽略该边否则加入到边的集合中
- 不断重复第二步,知道有 $V-1$条边
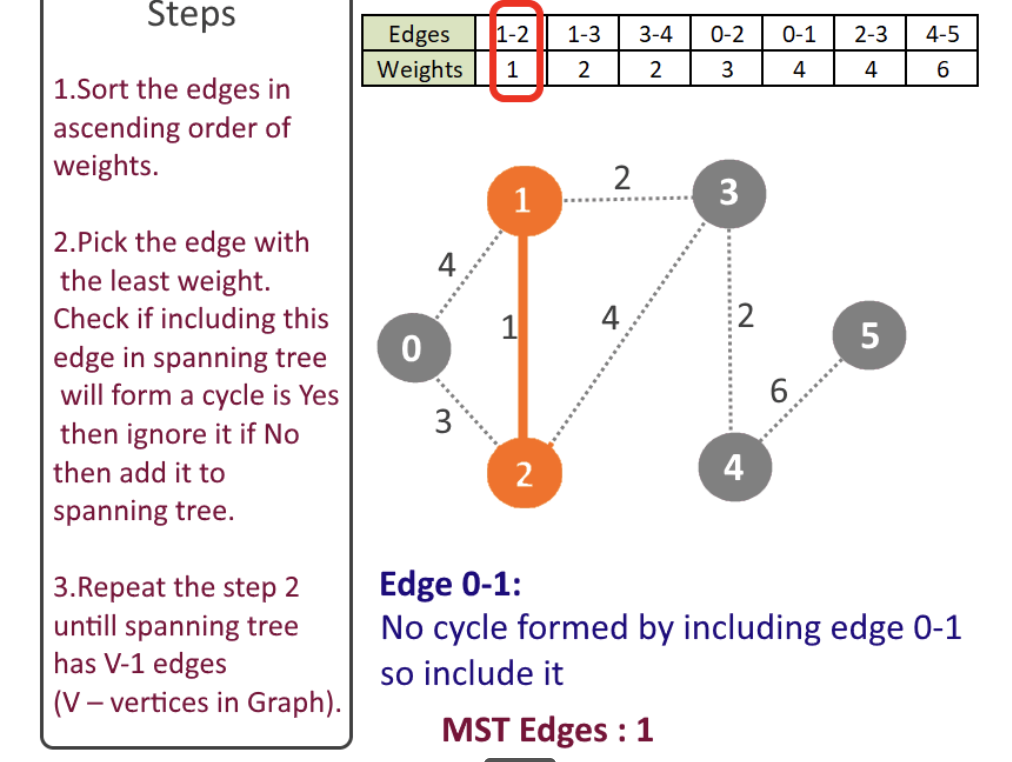
该网站提供了很好的动图显示上述过程。
适用于稠密图,时间复杂度 $O(n^2)$
核心思想:每次挑一条与当前集合相连的最短边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
|
2). Kruskal’s Minimal Spanning Tree Algorithm
Kruskal’s algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest. It is a greedy algorithm in graph theory as it finds a minimum spanning tree for a connected weighted graph adding increasing cost arcs at each step. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
Kruskal算法也是一种贪心算法。在无向有权连通图中,每次寻找权重最小的边,然后添加到集合中。
Prim’s algorithm 和Kruskal 的区别:
- 当边的权重都不相同时候,两个算法得到相同的结果
- 当边的权重存在相同,两个算法并不总是产生相同的结果
- Kruskal 算法适合稀疏图,即满足$E =O(V)$或者边更少; 边权已经排好序或者能够在线性时间内排序完成
- Prim 算法适合稠密图,即满足$E =O(V^2)$左右。
在算法步骤中的不同:
- Prim 在每一步骤中生成树总是相连的,Kruskal每一步中在通常情况下子树之间没有相连
- Prim 从任意一个顶点开始,然后加上和其相连最短边权的点,Kruskal每次加上最小权重的边到现有的树(森林)中
- Prim 算法在稠密图中更快,Kruskal在系数图中更快
适用于稀疏图,时间复杂度 $O(mlogm)$
核心思想:从小到大挑不多余的边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
|
(7) 最短路径
1). Dijkstra’s algorithm for shortest paths from a single source 单源最短路径问题
Dijkstra’s algorithm (or Dijkstra’s Shortest Path First algorithm, SPF algorithm) is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks.
Dijkstra’s迪杰斯特拉算法是计算两点之间的最短路径。(单源最短路径)
For a given source node in the graph, the algorithm finds the shortest path between that node and every other. It can also be used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined.
该算法是单源路径算法,给定源点,到达目的节点或者其余个各点的最短路径。
The Dijkstra algorithm uses labels that are positive integers or real numbers, which are totally ordered.
该算法要求结点的数值是非负。
时间复杂度 $O(mlogn)$, $n$表示点数,$m$表示边数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
|
1). Cheapest Flights Within K Stops
堆优化的Dijkstra求最短路,时间复杂度是$O(mlog(nK))$,其中$m$表示边的个数,$n$表示点的个数, $K$表示中转站的个数。这是一个双关键字最短路劲问题,$dis[i][j]$ 表示第$i$个点到达第$j$个点的最短的距离。如果使用普通队列,需要的时间复杂度是$O(mlogm)$。空间复杂度 邻接表需要$O(m)$空间,优先队列需要$O(m)$空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
struct Node {
int no, stops;
int distance;
Node(int no_, int stops_, int distance_): no(no_), stops(stops_), distance(distance_) {}
bool operator > (const Node &other) const {
return distance > other.distance;
}
};
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
const int INF = 1000000000;
vector<vector<pair<int, int>>> graph(n);
for (const auto &v: flights)
graph[v[0]].emplace_back(v[1], v[2]);
K++;
vector<vector<int>> dis(n, vector<int>(K + 1, INF));
vector<vector<bool>> vis(n, vector<bool>(K + 1, false));
priority_queue<Node, vector<Node>, greater<Node>> q;
q.push(Node(src, 0, 0));
dis[src][0] = 0;
while (!q.empty()) {
Node u = q.top();
q.pop();
if (vis[u.no][u.stops])
continue;
vis[u.no][u.stops] = true;
for (const auto &v: graph[u.no])
if (u.stops + 1 <= K && dis[v.first][u.stops + 1] > dis[u.no][u.stops] + v.second) {
dis[v.first][u.stops + 1] = dis[u.no][u.stops] + v.second;
q.push(Node(v.first, u.stops + 1, dis[v.first][u.stops + 1]));
}
}
int ans = INF;
for (int i = 1; i <= K; i++)
ans = min(ans, dis[dst][i]);
if (ans == INF)
ans = -1;
return ans;
}
};
|
python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution(object):
def findCheapestPrice(self, n, flights, src, dst, K):
"""
:type n: int
:type flights: List[List[int]]
:type src: int
:type dst: int
:type K: int
:rtype: int
"""
graph = {}
for flight in flights:
if flight[0] in graph:
graph[flight[0]][flight[1]] = flight[2]
else:
graph[flight[0]] = {flight[1]:flight[2]}
rec = {}
heap = [(0, -1, src)]
heapq.heapify(heap)
while heap:
cost, stops, city = heapq.heappop(heap)
if city == dst:
return cost
if stops == K or rec.get((city, stops), float('inf')) < cost:
continue
if city in graph:
for nei, price in graph[city].items():
summ = cost + price
if rec.get((nei, stops+1), float('inf')) > summ:
rec[(nei, stops+1)] = summ
heapq.heappush(heap, (summ, stops+1, nei))
return -1
|
2). Reachable Nodes In Subdivided Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
struct Node {
int x, d;
Node(int x_, int d_): x(x_), d(d_){}
bool operator < (const Node &v) const {
return d > v.d;
}
};
class Solution {
public:
void dijkstra(const vector<vector<pair<int, int>>>& e, int N, vector<int>& dis) {
priority_queue<Node> heap;
dis[0] = 0;
heap.push(Node(0, 0));
while (!heap.empty()) {
Node sta(heap.top());
heap.pop();
if (sta.d > dis[sta.x])
continue;
for (auto edge : e[sta.x]) {
if (dis[edge.first] > dis[sta.x] + edge.second) {
dis[edge.first] = dis[sta.x] + edge.second;
heap.push(Node(edge.first, dis[edge.first]));
}
}
}
}
int reachableNodes(vector<vector<int>>& edges, int M, int N) {
int m = edges.size();
const int inf = 200000000;
vector<vector<pair<int, int>>> e(m);
for (auto edge : edges) {
e[edge[0]].emplace_back(make_pair(edge[1], edge[2] + 1));
e[edge[1]].emplace_back(make_pair(edge[0], edge[2] + 1));
}
vector<int> dis(N, inf);
dijkstra(e, N, dis);
int ans = 0;
for (int i = 0; i < N; i++)
if (dis[i] <= M)
ans++;
for (auto edge : edges) {
int x = edge[0], y = edge[1];
if (dis[x] <= M && dis[y] <= M)
ans += min(edge[2], 2 * M - dis[x] - dis[y]);
else if (dis[x] <= M && dis[y] > M)
ans += min(edge[2], M - dis[x]);
else if (dis[y] <= M && dis[x] > M)
ans += min(edge[2], M - dis[y]);
}
return ans;
}
};
|
2). Floyd算法
In computer science, the Floyd–Warshall algorithm (also known as Floyd’s algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm) is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles).
Floyd 算法是任意两点之间的最短路径(多源);权重可以是负数,但是不能有负数的环。
时间复杂度是$O(V^3)$,其中$V$表示点的个数。Floyd是个动态规划,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
|
参考文献
- wiki Greedy_algorithm
- [leetcode 题目](

