基于隐马尔科夫的命名实体识别
文章目录
介绍自然语言处理中的命名实体识别(Named Entity Recognition,NER )相关概念,主要介绍基于HMM 的NER,包括HMM中的两大假设,三大参数和Viterbi 算法。
命名实体识别
序列标注简单来说就是给定一个序列, 然后对序列中的每一个元素做一个标记或者打一个标签,这是一个比较宽泛的概念。中文命名实体识别(NER)、中文分词和词性标注(part-of-speech tag, POS)等这些基本的NLP 任务都属于序列标注的范畴。中文命名实体识别问题就是将一段文本序列中包含我们感兴趣的实体识别出来,比如说人名、地名、机构名和时间等。
(1)定义
Named-entity recognition (NER) (also known as entity identification, entity chunking and entity extraction) is a subtask of information extraction that seeks to locate and classify named entity mentions in unstructured text into pre-defined categories such as the person names, organizations, locations, medical codes, time expressions, quantities, monetary values, percentages, etc. 给定一个句子,然后识别出句子中有意义的实体,比如说人名,机构名,地名,医药编码,时间表达,数量词,金钱表达和百分比。
命名实体识别主要分类,一般包括 3 大类(实体类、时间类和数字类)和 7 小类(人名、地名、组织名、机构名、时间、日期、货币和百分比)。但随着 NLP 任务的不断扩充,在特定领域中会出现特定的类别,比如医药领域中,药名、疾病等类别。
(2)发展脉络
1). 隐马尔可夫模型(Hidden Markov Model,HMM)
NER本质上可以看成是一种序列标注问题(预测每个字的BIOES标记),在使用HMM解决NER这种序列标注问题的时候,我们所能观测到的是字组成的序列(观测序列),观测不到的是每个字对应的标注(状态序列)。
解码问题,我们使用的是维特比(viterbi)算法。
2). 条件随机场(Conditional Random Field, CRF)
上面讲的HMM模型中存在两个假设,一是输出观察值之间严格独立,二是状态转移过程中当前状态只与前一状态有关。也就是说,在命名实体识别的场景下,HMM认为观测到的句子中的每个字都是相互独立的,而且当前时刻的标注只与前一时刻的标注相关。但实际上,命名实体识别往往需要更多的特征,比如词性,词的上下文等等,同时当前时刻的标注应该与前一时刻以及后一时刻的标注都相关联。由于这两个假设的存在,显然HMM模型在解决命名实体识别的问题上是存在缺陷的。
而条件随机场就没有这种问题,它通过引入自定义的特征函数,不仅可以表达观测之间的依赖,还可表示当前观测与前后多个状态之间的复杂依赖,可以有效克服HMM模型面临的问题。
解码的时候与HMM类似,也可以采用维特比算法。
3). Bi-LSTM
除了以上两种基于概率图模型的方法,LSTM也常常被用来解决序列标注问题。和HMM、CRF不同的是,LSTM是依靠神经网络超强的非线性拟合能力,在训练时将样本通过高维空间中的复杂非线性变换,学习到从样本到标注的函数,之后使用这个函数为指定的样本预测每个token的标注。
LSTM比起CRF模型最大的好处就是简单粗暴,不需要做繁杂的特征工程,直接训练即可,同时比起HMM,LSTM的准确率也比较高。
4). Bi-LSTM+CRF
CRF 是机器学习的方法,机器学习中困难的是如何构造和选择特征。Bi-LSTM属于深度学习算法,其优势在于不需要人为选择和构造特征。LSTM的优点是能够通过双向的设置学习到观测序列(输入的字)之间的依赖,在训练过程中,LSTM能够根据目标(比如识别实体)自动提取观测序列的特征,但是缺点是无法学习到状态序列(输出的标注)之间的关系,要知道,在命名实体识别任务中,标注之间是有一定的关系的,比如B类标注(表示某实体的开头)后面不会再接一个B类标注,所以LSTM在解决NER这类序列标注任务时,虽然可以省去很繁杂的特征工程,但是也存在无法学习到标注上下文的缺点。
相反,CRF的优点就是能对隐含状态建模,学习状态序列的特点,但它的缺点是需要手动提取序列特征。所以一般的做法是,在LSTM后面再加一层CRF,以获得两者的优点。
上述问题可以看成一个文本多分类的问题,按照道理讲使用一个语言模型应该是可以解决的,但是为什么还要加上概率图模型?
“自贸区"对应的标注是: 自(B-LOC)贸(I-LOC)区(I-LOC), 这三个字都对应一个"地名"的标签, 但是第一个字属于实体开头的字, 所以使用"B"开头的标签, 后面两个字的标签都是"I"开头.
当单独使用语言模型时候可能出现上述的问题。所以如果加上概率图模型,比如条件随机场,就可以约束模型的输出,防止出现不合规的标注输出。
5). BERT + CRF
目前主流的方式是通过一个语言模型(比如LSTM,BERT)+CRT(条件随机场)实现。那么BERT 作为一种语言模型,也是可以和CRF 结合起来进行NER 问题求解。
(3)评价指标
实际上NER 是对于字(或词)的多分类问题,所以分类中常用的评价指标如ACC,Precision-Recall和F1 同样适用于该场景。
(4)NER 的应用场景:
**新闻标注:**和文本分类不同, 这里可以使用NER技术将与文章相关的人物, 地点都以标签的形式标注出来, 方便用户对某个人物或地点进行索引。 **搜索引擎:**可以通过使用命名实体识别来抽取web页面中的实体, 后续可以使用这些信息来提高搜索效率和准确度。 从商品描述中自动提取商品类别, 品牌等信息, 提高货物上架效率, 在咸鱼等应用上已经实现了类似功能。 工具易用性提升, 例如从短信息或邮件中提取时间和地点等实体, 从而实现点击时间直接创建日历, 点击地址直接跳转到地图App等便捷操作。 一般来说 NER 是不使用在文本分类领域的。
(5)序列标注的两种模式
BIO B: 命名实体的起始 或 单个字命名实体 I: 命名实体的中间位置 或 结束位置 O:非命名实体
BIOES B: 命名实体的起始标注(Only哦) I: 命名实体的中间标注(Only哦) E: 命名实体的结尾标注(Only哦) O: 非命名实体 S: 单个字命名实体
(6)北大词性标注集部分标注词性如下表所示:
|
|
HMM
(1)定义
马尔科夫模型(markov model)
In probability theory, a Markov model is a stochastic model used to model randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it (that is, it assumes the Markov property). Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable. 在概率中,马尔科夫假设未来的状态仅仅由当前的状态决定,和其他的任何状态都无关。这种假设极大的简化了运算。
隐马尔科夫模型
A hidden Markov model is a Markov chain for which the state is only partially observable. In other words, observations are related to the state of the system, but they are typically insufficient to precisely determine the state. Several well-known algorithms for hidden Markov models exist. For example, given a sequence of observations, the Viterbi algorithm will compute the most-likely corresponding sequence of states, the forward algorithm will compute the probability of the sequence of observations, and the Baum–Welch algorithm will estimate the starting probabilities, the transition function, and the observation function of a hidden Markov model. 隐马尔科夫模型描述的是由不可观测的隐状态序列(实体标注)生成可观测状态(可读文本)的过程。使用前向传递算法计算观测序列的概率,使用viterbi 算法得到最优的标注徐磊,使用Baum-Welch 算法估计初始的状态,转移概率矩阵和发射矩阵。“隐"表示标注状态是不可见的。
(2)两大基本假设

- 第$t$个隐状态(实体标签)只跟前一时刻的$t-1$隐状态(实体标签)有关, 与除此之外的其他隐状态(如$t-2,\ t+3$)无关.
例如上图中: 蓝色的部分指的是$i_t$只与$i_{t-1}$有关, 而与蓝色区域之外的所有内容都无关, 而$P(i_{t}|i_{t-1})$指的是隐状态$i$从$t-1$时刻转向$t$时刻的概率, 具体转换方式下面会细讲. - 观测独立的假设, HMM模型中是由隐状态序列(实体标记)生成可观测状态(可读文本)的过程, 观测独立假设是指在任意时刻观测$o_t$只依赖于当前时刻的隐状态$i_t$, 与其他时刻的隐状态无关. 例如上图中: 粉红色的部分指的是$i_{t+1}$只与$o_{t+1}$有关, 跟粉红色区域之外的所有内容都无关.
(3)三大参数
- HMM的转移概率矩阵(transition probabilities)
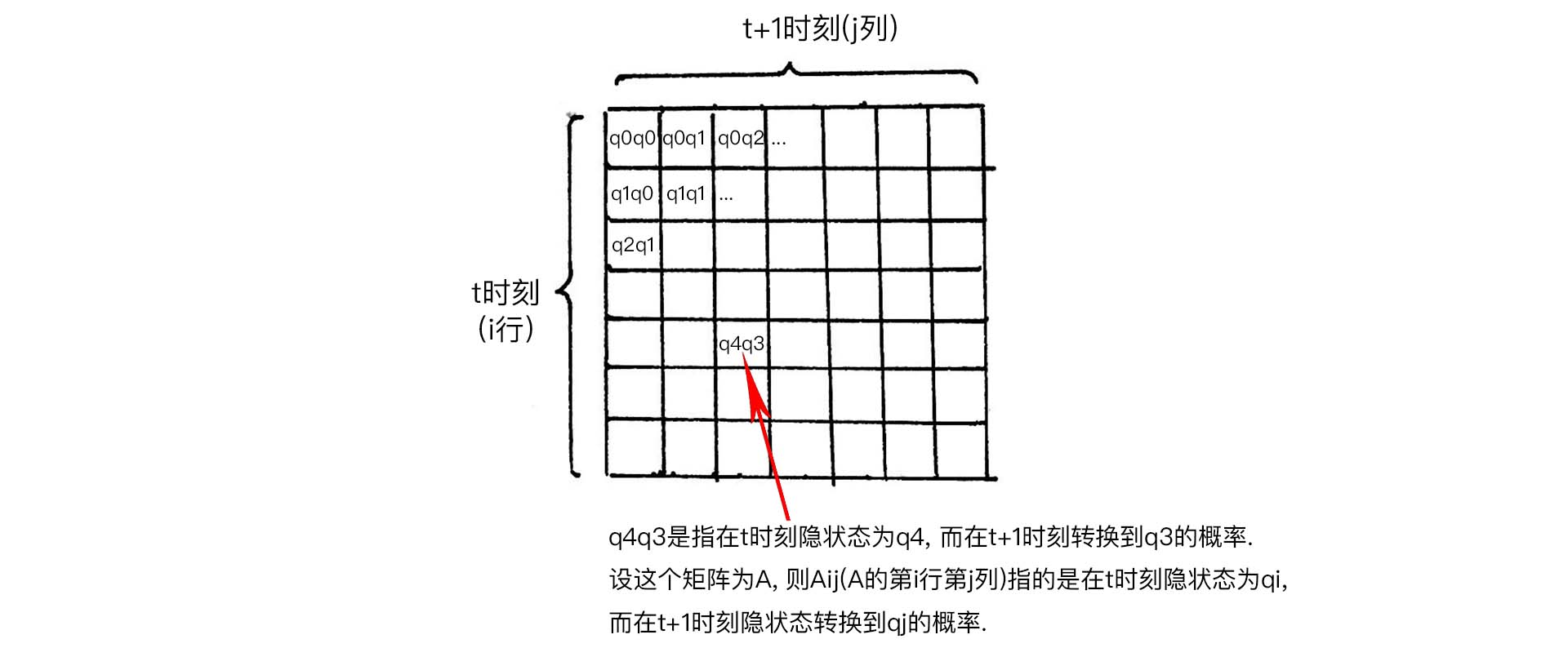
转移矩阵表示为$A$矩阵, 则$A_{ij}$表示矩阵中第i行第j列:
$$A_{ij}=P(i_{t+1}= q_j | i_{t} = q_i) \quad q_i \in Q_{hidden}$$
上式表示在$t$ 时刻的实体标签是 $q_i$, 在 $t+1$时刻的实体标签转换成了 $q_j$,概率表示为上式。
- HMM的发射概率矩阵(emission probabilities)
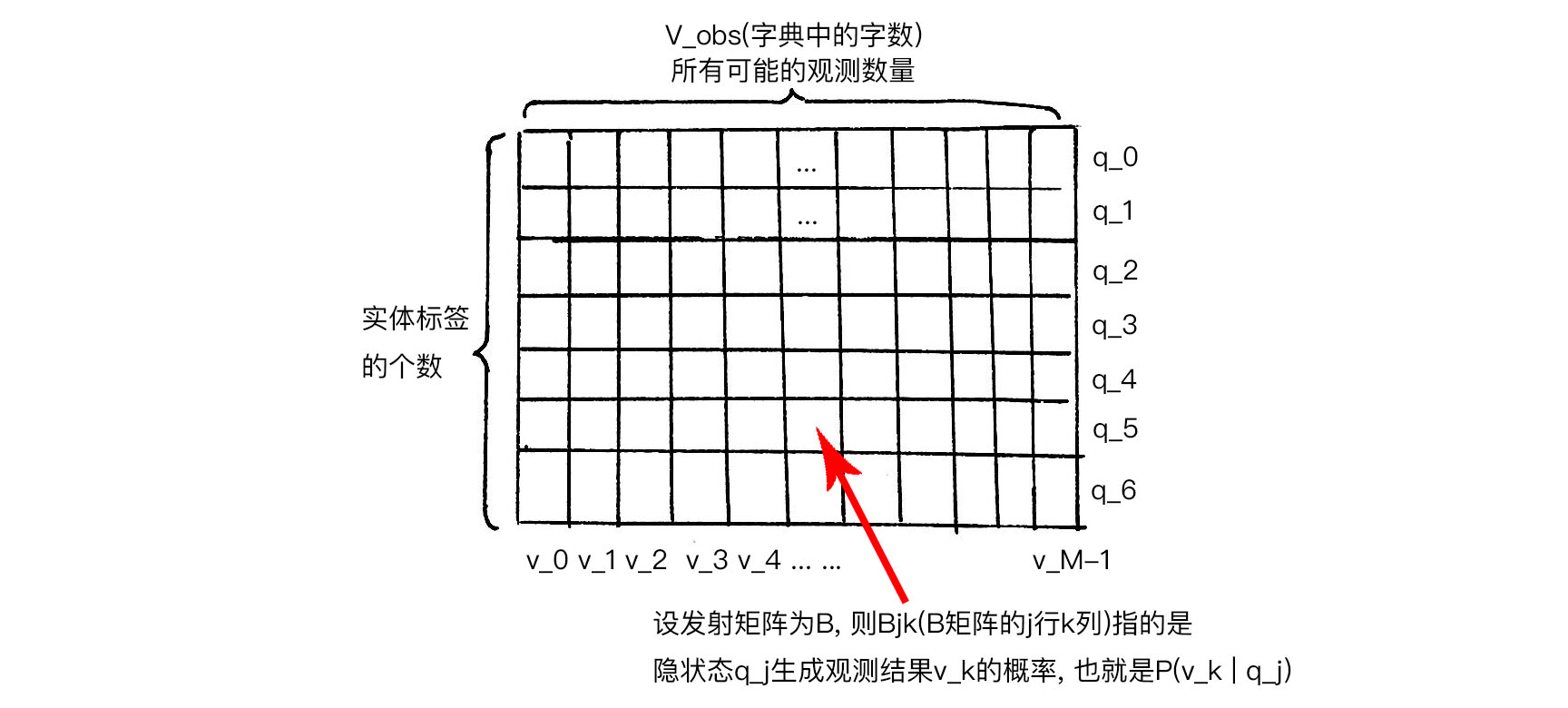
发射矩阵表示为$B$矩阵, 则$B_{jk}$表示矩阵中第$j$行第$k$列:
$$B_{jk}=P(o_{t}= v_k | i_{t} = q_j) \quad q_i \in Q_{hidden} \quad v_k \in V_{obs.}={v_0, v_1, … , v_{M-1} }$$
上式表示指的是在$t$时刻由实体标签(隐状态)$q_j$生成汉字(观测结果)$v_k$的概率.
- HMM的初始隐状态概率(initial probabilities)
通常用$\pi$来表示(不是圆周率):
$$\pi=P(i_1=q_i) \quad q_i \in Q_{hidden} = { q_0, q_1, … , q_{N-1}}$$
上式指的是**语言序列中第一个字**$o_1$的实体标记是$q_i$的概率, 也就是初始隐状态概率.
(4)Viterbi算法
1). 定义
The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models (HMM).
维特比算法(viterbi algorithm)使用的是动态规划的思想解决HMM 和CRF 中的预测问题。即在HMM模型中寻找最有可能的隐状态的路径。使用一句话概括为:在每一时刻,计算当前时刻是由上一个时刻中的每种隐状态导致的最大概率,并且记录这个最大概率是从前一时刻哪个隐状态转移过来的,最后回溯最大概率,即为路径。
2). 数学表达
- $A_{i, j}^{t-1, t}$, 是转移概率矩阵$A$中的第$i$行第$j$列(下标), 指的是在$t-1$时刻实体标签为$q_i$, 而在$t$时刻实体标签转换到$q_j$的概率.
- $B_{jk}$是发射矩阵的第j行第k列, 指的是在第$t$时刻, 由隐状态$q _j$生成观测$v _k$的概率.
- 有了上面两点, 则$\hat{q} _j = A _{ij}B _{jk}$表示在$t$时刻的隐状态为$q _j$的概率估计.
3). 计算过程
假设我们通过HMM建模并学习, 得到了模型所估计的参数$(A, B, \pi)$, 注意下面的$A, B$矩阵按行求和为$1$;

需要申请$T1, T2$两个表格:如果$T1, T2$表格是$i*j$的矩阵, 则矩阵中第$j$列指的是第$j$时刻, 第$i$行指的是第$i$种隐状态, $T1[i, \ j]$指的是在第$j$时刻, 落到隐状态$i$的最大可能的概率是多少(不要着急, 到了下一个时刻就会明白最大是什么意思), 而$T2[i, \ j]$记录的是这个最大可能的概率是从第$j-1$时刻(上一时刻)的哪一种隐状态$i$转移过来的, 也就是说我们记录的是最大可能的概率的转移路径.
我们现在将第一时刻的计算结果填入$T1, T2$表格, 注意在第$0$时刻的隐状态是由初始隐状态概率矩阵提供的, 而不是从上一时刻的隐状态转移过来的, 所以我们直接在$T2$表格上记为$NAN(not \ a \ number)$。然后计算表格上每个位置的最大概率。

4). 时间复杂度
假设有$N$种隐状态,在每个时刻之间,一共可能有 $N^2$种方式,假设有$T$时刻,那么viterbi 算法的时间复杂度$O(TN^2)$
分析代码
(1)数据处理部分
|
|
|
|
|
|
|
|
参考文献
文章作者 jijeng
上次更新 2019-09-06