Logistic & Softmax
文章目录
title: logistics 和softmax 的公式推导 date: 2019-07-05 20:37:41 categories: 机器学习
Logistics 和 softmax 的公式推导。总结常在面试过程中用到的公式推导。
Logistics公式推导
Logistics Regression 是线性分类器。所以还是先从线性回归中开始推导。LR 模型推导分成以下四个部分: 线性回归表示,sigmoid 激活函数、优化目标极大似然估计 和使用梯度上升的方式更新权重。
线性函数
$$
\begin{split}
h_{w}\left(x^{i}\right) &=w_{0}+w_{1} x_{1}+w x_{2}+\ldots+w_{n} x_{n} \\
h_{w}\left(x^{j}\right) &=w^{T} x_{i}=W^{T} X
\end{split}
$$
然后分别进行向量表示:
$$
\begin{split}
X &= \left[ 1 \ x_1 \ \dots x_n \right]^T \\
W &= \left[ w_0 \ w_1 \ \dots \ w_n \right]^T \\
\end{split}
$$
为了更好的表示分类模型,使用sigmoid 激活函数,引入了Logistics 回归。
逻辑回归是假设数据服从 Bernoulli 分布(抛硬币),因此LR属于参数模型。LR目标函数的定义:$$h_{\theta}(x)=g\left(\theta^{T} x\right)$$ 其中sigmoid 函数为:$g(z)=\frac{1}{1+e^{-z}}$。 sigmoid 函数的导数有很好的性质 $ g^{\prime}(z)=g(z)(1-g(z))$
似然函数
为什么这里会出现概率呢? 因为经过sigmoid 激活函数之后,会输出 $y_{pred}$, 范围是在 [0, 1] 之间,一般是跟军 0.5 去划分,如果大于 0.5 那么是 A 类,否则是B 类。 逻辑回归的优化目标是极大化对数似然估计,采用梯度上升来学习及更新参数$ \theta $向量的值。
假设有n个独立的训练样本 ${(x_1, y_1),(x_2, y_2), \ldots,(x_n, y_n)} $, 并且$ y ={ 0, 1} $。那每一个观察到的样本 $(x_i, y_i)$ 出现的概率是:
$$ P(y_i, x_i) = {P(y_i = 1| x_i)}^{y_i}{(1 -P(y_i =1| x_i)}^{1-y_i)} $$
推广到所有样本下,得到整体的似然函数表达,需要将所有的样本似然函数全部相乘。
$$ L(\theta) =\Pi{P(y_i = 1| x_i)}^{y_i}({1 -P(y_i =1| x_i)})^{1-y_i} $$
累乘的形式不利于进行优化分析,这里将似然函数取对数,得到对数似然函数,作为我们的最终优化目标,运用极大似然估计来求得最优的 $\theta$ (这个参数是来自线性相乘中的参数)
$$
\begin{split}
l(\theta) &=logL(\theta) \\
&= \sum_{i =1}^{m}(y^{(i)} \log h\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h\left(x^{(i)}\right)\right))
\end{split}
$$
最优化求解
使用链式法对目标函数进行求导然后求解。
$$ \frac{\partial}{\theta_{j}} J(\theta)=\frac{\partial J(\theta)}{\partial g\left(\theta^{T} x\right)} \times \frac{\partial g\left(\theta^{T} x\right)}{\partial \theta^{T} x} \times \frac{\partial \theta^{T} x}{\partial \theta_{j}} $$
分成三部分: 第一部分 $$ \frac{\partial J(\theta)}{\partial g\left(\theta^{T} x\right)}=y \times \frac{1}{g\left(\theta^{T} x\right)}+(y-1) \times \frac{1}{1-g\left(\theta^{T_{x} x}\right)} $$
第二部分
$$ \frac{\partial g\left(\theta^{T} x\right)}{\partial \theta^{T} x}=g\left(\theta^{T} x\right)\left(1-g\left(\theta^{T} x\right)\right) $$
第三部分
$$ \frac{\partial \theta^{T} x}{\theta_{j}}=\frac{\partial J\left(\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots \theta_{n} x_{n}\right)}{\partial \theta_{j}}=x_{j} $$
最后相乘可以得到:
$$ \frac{\partial}{\partial \theta_{j}} \ell(\theta)= \left(y-h_{\theta}(x)\right) x_{j}$$
因此总的 $\theta $ 的更新公式为: $$ J(\theta) := \theta_{j}+\alpha\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)}$$
关于logistics 的公式推导已经结束。
纯python 实现逻辑回归
线性分类器:模型是参数的线性函数,分类平面是(超)平面; 非线性分类器:模型分界面可以是曲面或者超平面的组合。 典型的线性分类器有感知机,LDA,逻辑斯特回归,SVM(线性核); 典型的非线性分类器有 kNN,决策树,SVM(非线性核)
关键是看后面,如何使用纯python 去实现一个逻辑回归。
代码:逻辑回归.py 讲解:机器学习算法 之逻辑回归以及python实现
在numpy 中,
|
|
softmax 的推导
多分类中使用的是交叉熵损失函数 ( cross entropy error function),交叉熵函数是凸函数。最后一层的网络展开,最终的结果展开成 one-hot 的形式,用 softmax 得到的概率值进行交叉熵的计算,带入公式
$$ J=-\sum_{c=1}^{M} y_{c} \log \left(p_{c}\right) $$
好好理解一下从softmax 到交叉熵计算过程。

这个里面有一部分关乎 softmax 的推导,但是感觉不是很全很详细:Logistics到softmax推导整理
SVM公式推导
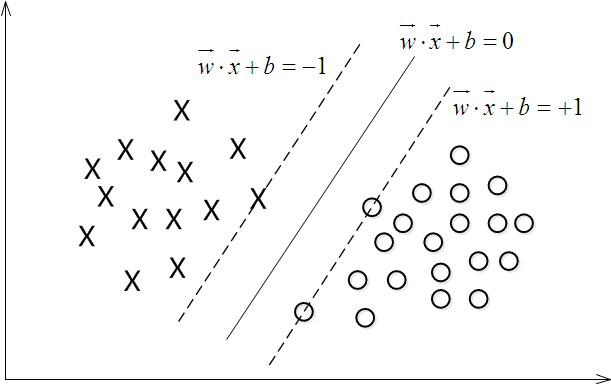
如上图中只有线上的点叫做支持向量,其他的点在 $y$ 中的表示要么是 1要么是-1。支持向量可以用来进行分类和回归,这里介绍的是分类问题。支持向量的目标是最大化正负样本之间的间隔。分类问题可以分成三类:
- 线性可分(硬间隔支持向量)
- 近似线性可分(软间隔支持向量,通过引入松弛变量实现)
- 线性完全不可分(使用非线性核函数)
下面的公式推导都是基于线性可分条件下的,也就是硬间隔支持向量机。步骤有二:
- 寻找最大分隔间距(原问题可以转换成对偶问题)
- 通过拉格朗日求解优化问题
从第一步中得到是一个二次规划问题,可以求解,但当样本量大的时候,计算量非常大,所以可以转换成其对偶问题求解。然后使用拉格朗日公式求解,这个时候引入一个参数拉格朗日参数,求解这个参数即可。
具体公式的推导可以参考下面的文章:
对于上面文章的解读
在样本空间,划分超平面可以通过以下线性方程描述: $$w^Tx+b =0$$ 假设超平面 $(w,b) $能将训练样本正确分类,即对于$(x_i,y_i)∈D $,若 $y_i=+1$,则有 $w^Tx+b>0 $;若 $y_i=−1$ (这个条件是假设的,令)
- 从原来的分段函数表示成下面的公式,在于这样的结果是可以直接表示分类结果的正确与否,如果结果大于0表示 $f(x)$ 和 $label $ 是同号,那么表示预测正确,否则预测错误。
$$ y_{i} \cdot\left(w^{T} x_{i}+b\right) \geq 1 $$
公式中的 1-5 对应的是步骤一;步骤6-10 是对应求解问题。
-
在计算过程中支持向量的点是用来计算距离的,其他样本点是体现在约束条件中。
-
判别模型
反向传播的推导
这个推导也是超级简单,分成三个步骤:
- 前向传播,注意$f_1$ 和 $y_1$ 所表示的含义的不同,前者经过激活函数 比如说sigmoid 就得到了后者
- 反向传播,和前向传播是一样的,只不过出发点是 $\delta$,关键是要使用到前面的weight 信息进行 $\delta$ 的重新分配
- 权值更新,注意涉及到原来的 weights、error、梯度和学习率四个变量。
(注意在权值更新推导的时候,一定要使用到学习率,求导,error 这几个变量,否则是没有办法基于之前的进行更新的) 详细情况可以看这里
xgboost 中的理论推导
xgboost 的loss 的二阶展开推导

上面式子中的 loss包含着正则项。
- 一个是树里面叶子节点的个数T
- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)

泰勒二阶展开式:
$$ f(x+\Delta x) \simeq f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2} $$
XGBoost与GBDT有什么不同
- GBDT是机器学习算法,XGBoost是该算法的工程实现。
- 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
- GBDT在模型训练时只使用了代价函数的一阶导数信息(随机梯度下降),XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。(牛顿法)
- 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
- 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
- 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
- XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
- XGBoost在训练的过程中给出各个特征的评分,从而表明每个特征对模型训练的重要性。XGBoost利用梯度优化模型算法, 样本是不放回的,想象一个样本连续重复抽出,梯度来回踏步,这显然不利于收敛。XGBoost支持子采样, 也就是每轮计算可以不使用全部样本。
(XGBoost详解)[https://www.jianshu.com/p/ac1c12f3fba1]
文章作者 jijeng
上次更新 2019-10-22