Loss Function
文章目录
介绍激活函数(activation function)、损失函数(loss function)和在pytorch框架下的使用。
Activation Function
What?
It’s just a thing (node) that you add to the output end of any neural network. It is also known as Transfer Function. It can also be attached in between two Neural Networks.
$$ Output = activation function \left( x _ { 1 } w _ { 1 } + x _ { 2 } w _ { 2 } + \cdots + x _ { n } w _ { n } + b i a s \right) $$
A weighted sum is computed as: $$ x _ { 1 } w _ { 1 } + x _ { 2 } w _ { 2 } + \cdots + x _ { n } w _ { n } $$ Then, the computed value is fed into the activation function, which then prepares an output. $$ activation function \left( x _ { 1 } w _ { 1 } + x _ { 2 } w _ { 2 } + \cdots + x _ { n } w _ { n } + b i a s \right) $$
Think of the activation function as a mathematical operation that normalises the input and produces an output. The output is then passed forward onto the neurons on the subsequent layer.
The major purpose of activation function in neural networks is to introduce non-linearity between output and the input. They basically decide when to fire a neuron and when to not. If we do not use activation fucntion, there will be a linear relationship between input and output variables and it would not be able to solve much complex problems as a linear relationship has some limitations. The main objective of introducing a activation function is to introduce non-linearity which should be able to solve complex problems such as Natural Language Processing, Classification, Recognition, Segmentation etc.
激活函数的主要目的是增加网络的非线性。
The thresholds are pre-defined numerical values in the function. This very nature of the activation functions can add non-linearity to the output.
Activation Function Types
sigmoid 和 tanh 都是饱和激活函数;relu 及其变体都是非饱和函数。
Linear Activation Function: $$ output = k * x $$ where $k$ is a scalar value, as an instance 2, and $x$ is the input.

**Sigmoid or Logistic Activation Function **
The sigmoid activation function is “S” shaped. It can add non-linearity to the output and returns a binary value of 0 or 1.
$$ Output = \frac { 1 } { 1 + e ^ { - x } } $$
 这个函数有一个很好的导数形式,在反向传播的时候,效果比较明显。
这个函数有一个很好的导数形式,在反向传播的时候,效果比较明显。
|
|
Tanh Activation Function
Tanh is an extension of the sigmoid activation function. Hence Tanh can be used to add non-linearity to the output. The output is within the range of -1 to 1. Tanh function shifts the result of the sigmoid activation function:
$$ \text { Output } = \frac { 2 } { 1 + e ^ { - 2 x } } - 1 $$

Rectified Linear Unit Activation Function (RELU)
RELU is one of the most used activation functions. It is preferred to use RELU in the hidden layer. The concept is very straight forward. It also adds non-linearity to the output. However the result can range from 0 to infinity.
$$
Output = \max ( 0 , x )
$$
 这个是很高的评价了。
If you are unsure of which activation function you want to use then use RELU.
这个是很高的评价了。
If you are unsure of which activation function you want to use then use RELU.
在pytorch
|
|
但是问题在于负值容易引起神经死亡,每次遇到负值部分,激活函数都是为0.
斜坡函数,引入了非线性,可以对抗梯度消失/爆炸问题,相对而言计算效率也更高。
Relu6
Given an input x, ReLU6 will take the maximal value between 0 and x, then the minimal value between the initial output and 6.
这个是比较简单,数学表达式:
$$ Output =\min( \max ( 0 , x ), 6) $$
主要用在 mobilnet 网络中,因为该网络是为了移动端设备 float16 /int8 低精度时候也可以有较好的数值分辨率,所以对每层的网络输出值进行限制,因为低精度是无法精确表示之前如此大范围的数值,会带来精度损失。
Leaky Relu
为了处理负值问题,Relu 有了变种,表达式为 $$ Output = \max ( 0.01 *x , x ) $$
解决了当 $x<0$时候,网络死亡的问题。
|
|
Pre Relu
为了处理负值问题,Relu 有了变种,表达式为 $$ Output = \max ( a *x , x ) $$
解决了当 $x<0$时候,网络死亡的问题。其中的超参数$a$ 是可以调整的。
|
|
Swish

Swish is simple - it’s $x$ times the sigmoid funciton. $$ Output = x * \frac { 1 } { 1 + e ^ { - \beta x } } $$
其中 $\beta$ 在网络中被设置成可学习参数,在上图中 $\beta =1$

因此,Swish激活函数可以看作是介于线性函数与ReLU函数之间的平滑函数。当β被设置为可训练参数时,内插程度可以由模型控制。原论文中称之为Swish-β。
Like ReLU, Swish is bounded below and unbounded above. However, unlike ReLU, Swish is smooth (it does not have sudden changes of motion or a vertex) . Additionally, Swish is non-monotonic, meaning that there is not always a singularly and continually positive (or negative) derivative throughout the entire function. ( Restated, the Swish function has a negative derivative at certain points and a positive derivative at certain points and a positive derivative at other points, instead of only a positive derivative at all points, like Softplus or Sigmoid.)
目前研究,许多优秀的激活函数都是 unbounded above,比如说 relu 系列. Swish 具有非单调性 和光滑性。
相比于 relu,Swish 是平滑且非单调的函数,这点就能和很多激活函数分离开来。
Unboundedness is desirable for activation funcions becauseis avoids a slow training time during near-zero gradients - functions lke sigmoid or tanh are bounded above and below, so the network needs to be carefully initialized to stay within the limitations of these functions.
Being bounded below may be advantages becase of strong regularization - functions that approach zero in a limit to negative infinity are great at regularization because large negative inputs are discarded. This is important at the begining of training when large negative activation inputs are common.
分析值域上限和下限对网络学习的影响
实验结果

从上面分析,当 layer 数量大于42 Swish 效果比较好;在batch size 128 到 2048 这样的维度,Swish 都是比较好的。
Google 在多个难度较高的数据集上进行实验,证明 Swish 激活函数在深层模型上的效果优于 Relu。仅仅替换 Relu 就有提升,相对而言性价比还是很高的。
Research by the authors of the papers shows that simply be substituting ReLU units with Swish units improves the best classification accuracy on ImageNet by 0.9% for Mobile NASNet-A and 0.6% for Inception-ResNet-v2.
参考论文:
SWISH:A SELF-GATED ACTIVATION FUNCTION
更加新的论文介绍激活函数 Mish:https://arxiv.org/pdf/1908.08681.pdf (19年)
是基于 swish 进行改进的 loss function
Elu Exponential Line Unit
$$
\text{ELU}(x) = \max(0,x) + \min(0, \alpha * (\exp(x) - 1))`.
$$
 继承了Relu的所有优点,but贵一点,均值为0的输出、而且处处一阶可导。
继承了Relu的所有优点,but贵一点,均值为0的输出、而且处处一阶可导。
**Softmax Activation Function **
Softmax is an extension of the Sigmoid activation function. Softmax function adds non-linearity to the output, however it is mainly used for classification examples where multiple classes of results can be computed.
$$ Output = \frac { e ^ { x } } { \operatorname { sum } \left( e ^ { x } \right) } $$
这个一般使用在最后,作为多分类的结束。
Loss Function(Error Function)
机器学习中所有的算法都需要最大化或最小化一个函数,这个函数被称为“目标函数”。其中,我们一般把最小化的一类函数,称为“损失函数”。它能根据预测结果,衡量出模型预测能力的好坏。
损失函数 (Loss function) 是用来衡量模型的预测值 $f(x)$ 和真实值 $Y$ 的不一样的程度,通常使用 $L (Y, f(x))$ 来进行表示,损失函数越小,模型的鲁棒性越强。
选择loss 的时候需要考虑两点:分类or 回归问题 和结果的输出情况。
the choice of loss function must match the framing of the specific predictive modeling problem, such as classification or regression. Further, the configuration of the output layer must also be appropriate for the chosen loss function.
总的来说是可以分成三类:回归模型,二分类模型和多分类模型
-
Regression Loss Functions a. Mean Squared Error Loss b. Mean Squared Logarithmic Error Loss c. Mean Absolute Error Loss
-
Binary Classification Loss Functions a. Binary Cross-Entropy b. Hinge Loss c. Squared Hinge Loss
-
Multi-Class Classification Loss Functions a. Multi-Class Cross-Entropy Loss b. Sparse Multiclass Cross-Entropy Loss c. Kullback Leibler Divergence Loss
Regression Loss Function
如何进行选择?
对于回归问题,一个baseline 的loss function 是可以选择平方损失函数。从数据的角度进行分析,如果数据服从正太分布,那么平方损失函数没有问题,如果数据有一些 outlier,可以使用 mean squared logarithmic error loss, 先进行 $\hat { y } $然后再计算平方和。如果 outlier 比较多的话,那么使用 mean absolute error loss,计算差值的时候换成绝对值函数。
平方损失函数
Mean Squared Error (MSE), or quadratic, loss function is widely used in linear regression as the performance measure, and the method of minimizing MSE is called Ordinary Least Squares (OSL)。
To calculate MSE, you take the difference between your predictions and the ground truth, square it, and average it out across the whole dataset.
$$ Loss = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( y ^ { ( i ) } - \hat { y } ^ { ( i ) } \right) ^ { 2 } $$
在线性回归中,它假设样本和噪声都服从高斯分布(为什么假设成高斯分布呢?其实这里隐藏了一个小知识点,就是中心极限定理),最后通过极大似然估计MLE可以推导出最小二乘式子,即平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到。
$$ S E = \sum _ { i = 1 } ^ { n } \left( y _ { i } - y _ { i } ^ { p } \right) ^ { 2 } $$
为什么选择欧式距离作为误差的度量?
- 简单,计算方便
- 欧式距离是一种很好的相似度衡量标准
- 在不同的表示域变换之后,特征的性质能够保持不变。
在实际应用中,通常会使用 均方差作为一种衡量指标,就是在上面的公式中除以 N.
使用说明:
如果 target 是服从高斯分布,那么使用 mean squared error 是没有问题;并且没有很好的理由进行替换的话,那么就是他了。
Mathematically, it is the preferred loss function under the inference framework of maximum likelihood if the distribution of the target variable is Gaussian. It is the loss function to be evaluated first and only changed if you have a good reason.
Mean Squared Logarithmic Error Loss
和上面的的 mse 有一点差别。这个是先记性 log 求结果,然后再计算 mse.
you can first calculate the natural logarithm of each of the predicted values, then calculate the mean squared error. This is called the Mean Squared Logarithmic Error loss, or MSLE for short.
好处: It has the effect of relaxing the punishing effect of large differences in large predicted values.
使用说明: 如果最后的结果的数值有大值,那么可以尝试一下。不是那么符合高斯分布,就可以尝试一下。
均方差误差数学表达为: $$ \begin{equation} \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} \end{equation} $$
或者 $$ \begin{equation} \frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} \end{equation} $$
其中 $\bar{X} = \frac{X_1 + \dots + X_n}{n}$。
在pytorch 中使用nn.MSELoss 实现。首先定义了二维数组用于计算:
|
|
|
|
Mean Absolute Error Loss
定义: Mean Absolute Error (MAE) is a quantity used to measure how close forecasts or predictions are to the eventual outcomes, which is computed by $$ Loss = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left| y ^ { ( i ) } - \hat { y } ^ { ( i ) } \right| $$
where $| .|$ denotes the absolute value. Albeit, both MSE and MAE are used in predictive modeling, there are several differences between them. MSE has nice mathematical properties which makes it easier to compute the gradient. However, MAE requires more complicated tools such as linear programming to compute the gradient. Because of the square, large errors have relatively greater influence on MSE than do the smaller error. Therefore, MAE is more robust to outliers since it does not make use of square. On the other hand, MSE is more useful if concerning about large errors whose consequences are much bigger than equivalent smaller ones. MSE also corresponds to maximizing the likelihood of Gaussian random variables.
使用说明:
当有很多的点偏离 mean and variance 的时候,可以尝试使用 mae loss function,这个显著的特点在于 对outlier 是有抵抗作用的。
The Mean Absolute Error, or MAE, loss is an appropriate loss function in this case as it is more robust to outliers. It is calculated as the average of the absolute difference between the actual and predicted values.
在pytorch 中使用 nn.L1Loss 使用(因为绝对值损失又叫做L1 损失)
|
|
基于绝对值损失改进的是SmoothL1Loss (也叫做 Huber Loss), 其在(-1,1) 上是平方损失,其他情况是 L1 损失。
|
|
Binary Classification Loss Function (二分类)
Binary Cross-Entropy Loss
Cross-entropy loss is often simply referred to as “cross-entropy,” “logarithmic loss,” “logistic loss,” or “log loss” for short.
Cross-entropy is the default loss function to use for binary classification problems. 如果没有更好的二分类的选择(理由),那么这个就是首选。
数学定义:
Cross-entropy will calculate a score that summarizes the average difference between the actual and predicted probability distributions for predicting class 1. The score is minimized and a perfect cross-entropy value is 0.
使用说明:
Mathematically, it is the preferred loss function under the inference framework of maximum likelihood. It is the loss function to be evaluated first and only changed if you have a good reason. It is intended for use with binary classification where the target values are in the set {0, 1}.
在pytorch 中 nn.CrossEntropyLoss()是nn.logSoftmax()和 nn.NLLLoss()的整合。损失函数计算如下:
$$ \begin{equation} \operatorname{loss}(x, \text { class })=-\log \left(\frac{\exp (x[\text { class }])}{\sum_{j} \exp (x[j])}\right)=-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right) \end{equation} $$
其中 $C$ 表示类别数。损失函数中也有权重weight参数设置,针对样本不均衡的情况下,是有优化效果的。 $$ \begin{equation} \operatorname{loss}(x, \text { class })= \text{weight}[\text{class}] (-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right)) \end{equation} $$
需要注意的是,target输入必须是 tensor long 类型(int64位)
|
|
其中这里的 input 在实际的模型中是 $y_{pred}$, 而 target 是是标签类比的index。上面的代码等价于
|
|
在pytorch 中使用该损失函数,前面是不需要加 softmax 层。
负对数似然损失函数(Negative Log Likelihood)
同样适用于多类分类器,使用 nn.NLLLoss 实现,如果最后一层使用了log softmax 处理,那么就直接使用 nn.NLLLoss。经过了logSoftmax 得到的结果和
|
|
和下面是等价的
|
|
NLLLoss : negative log likelihood
对softmax 之后的数值,取log,然后再取负,得到正值,然后求解平均数。
Hinge Loss
An alternative to cross-entropy for binary classification problems is the hinge loss function, primarily developed for use with Support Vector Machine (SVM) models.
Hinge Loss,又称合页损失,其表达式如下:
$$ Loss = \max ( 0,1 - y s ) $$ 其中 y 和 s 的取值范围都是 [-1, 1]. 想想 SVM 中最大化间隔的内容就理解了。图像如下:
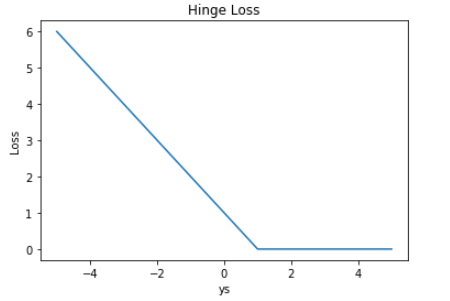
如同合起来的书,所以称之为 合页损失。显然,只有当 ys < 1 时,Loss 才大于零;对于 ys > 1 的情况,Loss 始终为零。Hinge Loss 一般多用于支持向量机(SVM)中,体现了 SVM 距离最大化的思想。 而且,当 Loss 大于零时,是线性函数,便于梯度下降算法求导。Hinge Loss 的另一个优点是使得 ys > 0 的样本损失皆为 0,由此带来了稀疏解,使得 SVM 仅通过少量的支持向量就能确定最终超平面。
使用说明: 要求 target 转换成 {-1, 1} ,效果有时候比 cross-binary 要好。
It is intended for use with binary classification where the target values are in the set {-1, 1}. Reports of performance with the hinge loss are mixed, sometimes resulting in better performance than cross-entropy on binary classification problems.
( 这句话比较迷离呀)
The hinge loss function encourages examples to have the correct sign, assigning more error when there is a difference in the sign between the actual and predicted class values.
**Squared Hinge Loss **
(通常上讲,最后的结果更加光滑是没有什么劣势的) A popular extension is called the squared hinge loss that simply calculates the square of the score hinge loss. It has the effect of smoothing the surface of the error function and making it numerically easier to work with.
需要从 {0, 1} -> {-1, 1} 这样target 的转换, 非常容易实现。
|
|
使用说明:
(很强的相关性了) If using a hinge loss does result in better performance on a given binary classification problem, is likely that a squared hinge loss may be appropriate.
Multi-Class Classification Loss Functions
对于多类问题的定义:
The problem is often framed as predicting an integer value, where each class is assigned a unique integer value from 0 to (num_classes – 1). The problem is often implemented as predicting the probability of the example belonging to each known class.
**Multi-Class Cross-Entropy Loss **
Cross-entropy is the default loss function to use for multi-class classification problems. (可见 交叉熵对于分类问题的重要性)
同理,如果是最大似然,概率模型,donot hesitate.( 数学基础就是在这里) Mathematically, it is the preferred loss function under the inference framework of maximum likelihood. It is the loss function to be evaluated first and only changed if you have a good reason.
Cross-entropy will calculate a score that summarizes the average difference between the actual and predicted probability distributions for all classes in the problem. The score is minimized and a perfect cross-entropy value is 0.
基于 keras实现的时候需要先把 target (label) 转成 one-hot 类型的,当然这个可能造成 loss 曲线的波动(后话)。
|
|
Sparse Multiclass Cross-Entropy Loss
和上面的区别主要在于 label 是不需要转成 one-hot 类型的,保持这原来的 number 形式。 Sparse cross-entropy addresses this by performing the same cross-entropy calculation of error, without requiring that the target variable be one hot encoded prior to training.
Kullback Leibler Divergence Loss
Kullback Leibler Divergence, or KL Divergence for short, is a measure of how one probability distribution differs from a baseline distribution.
数学原理:(以 bit 为单位的 信息熵)
A KL divergence loss of 0 suggests the distributions are identical. In practice, the behavior of KL Divergence is very similar to cross-entropy. It calculates how much information is lost (in terms of bits) if the predicted probability distribution is used to approximate the desired target probability distribution.
使用说明:更常使用 在复杂的模型上,比如 dense representation 之列。当然也是可以使用在多分类的情况下,这个时候如同 multi-class cross-entropy.
As such, the KL divergence loss function is more commonly used when using models that learn to approximate a more complex function than simply multi-class classification, such as in the case of an autoencoder used for learning a dense feature representation under a model that must reconstruct the original input. In this case, KL divergence loss would be preferred. Nevertheless, it can be used for multi-class classification, in which case it is functionally equivalent to multi-class cross-entropy.
参考文献:
How to Choose Loss Functions When Training Deep Learning Neural Networks
**log 对数损失函数 **
在逻辑回归的推导中,它假设样本服从伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着取对数求极值等等。
**指数损失函数 **
公式如下: $$ loss = e ^ { - y s } $$
曲线如下:

Exponential Loss 与交叉熵 Loss 类似,但它是指数下降的,因此梯度较其它 Loss 来说,更大一些。 Exponential Loss 一般多用于AdaBoost 中。因为使用 Exponential Loss 能比较方便地利用加法模型推导出 AdaBoost算法。
$$ L = - \log \frac { e ^ { s } } { \sum _ { j = 1 } ^ { C } e ^ { s _ { j } } } = - s + \log \sum _ { j = 1 } ^ { C } e ^ { s _ { j } } $$
softmax loss 的曲线如下图所示:

上图中,当 s « 0 时,Softmax 近似线性;当 s»0 时,Softmax 趋向于零。Softmax 同样受异常点的干扰较小,多用于神经网络多分类问题中。
若我们把 ys 的坐标范围取得更大一些,上面 5 种 Loss 的差别会更大一些,如图:

显然,这时候 Exponential Loss 会远远大于其它 Loss。从训练的角度来看,模型会更加偏向于惩罚较大的点,赋予其更大的权重。如果样本中存在离群点,Exponential Loss 会给离群点赋予更高的权重,但却可能是以牺牲其他正常数据点的预测效果为代价,可能会降低模型的整体性能,使得模型不够健壮(robust)。
相比 Exponential Loss,其它四个 Loss,包括 Softmax Loss,都对离群点有较好的“容忍性”,受异常点的干扰较小,模型较为健壮。
**Softmax loss **
对于多分类问题,可以使用 softmax loss。
其中,C 为类别个数,小写字母 s 是正确类别对应的 Softmax 输入,大写字母 S 是正确类别对应的 Softmax 输出。
由于 log 运算符不会影响函数的单调性,我们对 S 进行 log 操作。另外,我们希望 log(S) 越大越好,即正确类别对应的相对概率越大越好,那么就可以对 log(S) 前面加个负号,来表示损失函数:
如何选择损失函数?
对于异常点的处理是一个维度,比如L1 损失函数处理异常点更加稳定,相对L2 损失函数。
what?
衡量模型好坏的 function,如果模型表现好,那么loss 应该是小;如果模型表现不好,那么loss 应该是大的。
At its core, a loss function is incredibly simple: it’s a method of evaluating how well your algorithm models your dataset. If your predictions are totally off, your loss function will output a higher number. If they’re pretty good, it’ll output a lower number. As you change pieces of your algorithm to try and improve your model, your loss function will tell you if you’re getting anywhere.
Log Loss (Cross Entropy Loss)
Cross-entropy loss, or log loss, measures the performance of a classification model whose output is a probability value between 0 and 1. Cross-entropy loss increases as the predicted probability diverges from the actual label. So predicting a probability of .012 when the actual observation label is 1 would be bad and result in a high loss value. A perfect model would have a log loss of 0.

The graph above shows the range of possible loss values given a true observation (isDog = 1). As the predicted probability approaches 1, log loss slowly decreases. As the predicted probability decreases, however, the log loss increases rapidly. Log loss penalizes both types of errors, but especially those predictions that are confident and wrong!
Cross-entropy and log loss are slightly different depending on context, but in machine learning when calculating error rates between 0 and 1 they resolve to the same thing.
In binary classification, where the number of classes M equals 2, cross-entropy can be calculated as:
$$
- ( y \log ( y ) + ( 1 - y ) \log ( 1 - y ) ) $$
If $ M>$2 (i.e. multiclass classification), we calculate a separate loss for each class label per observation and sum the result.
$$
- \sum _ { c = 1 } ^ { M } y _ { o , c } \log \left( y _ { o , c } \right) $$
M - number of classes (dog, cat, fish) log - the natural log y - binary indicator (0 or 1) if class label c is the correct classification for observation o
想要表达的是 log loss 是从 Likelihood Loss,改进过来的,有没有发现最大似然的痕迹。
log loss 表达式如下:
$$
\begin{split}
P(Y | X) &= P(X_1 | Y) \times P(X_2 | Y) \times \dots \times P(X_n | Y) \times P(Y) = P(Y) \prod_{i}^{n} P(X_i | Y) \\
&\Rightarrow log(P(Y | X)) = log(\prod_{i}^{n} P(X_i | Y) \Rightarrow \sum_{i}^{n} log(P(X_i | Y))
\end{split}
$$
交叉熵表达式:
$$CE(\hat{y}, y) = - \sum_{i=1}^{n} y_i log(\hat{y}) + (1 - y_i) log(1 - \hat{y})$$
L2
这两个loss function 在这里介绍过,所以本博客中简单说一下。
L2 loss function is the square of the L2 norm of the difference between actual value and predicted value. It is mathematically similar to MSE, only do not have division by n, it is computed by
$$ Loss = \sum _ { i = 1 } ^ { n } \left( y ^ { ( i ) } - \hat { y } ^ { ( i ) } \right) ^ { 2 } $$
Kullback Leibler (KL) Divergence (计算的是两个分布的问题) KL Divergence, also known as relative entropy, information divergence/gain, is a measure of how one probability distribution diverges from a second expected probability distribution. KL divergence loss function is computed by $$ D _ { K L } ( p | q ) = \sum _ { x } p ( x ) \log \frac { p ( x ) } { q ( x ) } $$
交叉熵的定义:
$$
H ( p , q ) = - \sum _ { x } p ( x ) \log q ( x )
$$
两者的关系推导,
$$
\begin{split}
D _ { K L } ( p | q ) &= \sum _ { x } p ( x ) \log \frac { p ( x ) } { q ( x ) } \\
&= \sum _ { x } ( p ( x ) \log p ( x ) - p ( x ) \log q ( x ) ) \\
&= - H ( p ) - \sum _ { x } p ( x ) \log q ( x ) \\
&= - H ( p ) + H ( p , q )
\end{split}
$$
所以说, cross entropy 也是可以写成这样:
$$
H ( p , q ) = D _ { K L } ( p | q ) + H ( p )
$$
logistic loss 和 cross entropy的关系
当 $ p \in { y , 1 - y }$, $q \in { \hat { y } , 1 - \hat { y } }$ ,cross entropy 可以写成 logistic loss:
$$ H ( p , q ) = - \sum _ { x } p ( x ) \log q ( x ) = - y \log \hat { y } - ( 1 - y ) \log ( 1 - \hat { y } ) $$
交叉熵函数是怎么来的?
从上面可以清楚的了解到,交叉熵函数在分类问题上是 default 的选择,那么我们有没有思考过 这个loss function 的数学基础 ?是怎么来的呢?
真实的样本标签为 [0, 1], 分别表示负类和正类,模型最终会经过一个 sigmoid 函数,输出一个概率值。sigmoid 函数的表达式如下: $$ g ( s ) = \frac { 1 } { 1 + e ^ { - s } } $$
所以sigmoid 的输出值表示 1的概率: $$ \hat { y } = P ( y = 1 | x ) $$ 表示 0的概率: $$ 1 - \hat { y } = P ( y = 0 | x ) $$
进而,从最大似然的角度出发,将上面的两种情况整合起来:
$$ P ( y | x ) = \hat { y } ^ { y } \cdot ( 1 - \hat { y } ) ^ { 1 - y } $$
从另一个角度也可以理解这个公式,分别令 y =0 和y =1, 发现两种情况正好对应着 $P ( y = 0 | x ) = 1 - \hat { y }$ 和 $P ( y = 1 | x ) = \hat { y }$。 我们做的就是把上面两种情况给整合起来了。
接下来引入 log 函数 $$ \log P ( y | x ) = \log \left( \hat { y } ^ { y } \cdot ( 1 - \hat { y } ) ^ { 1 - y } \right) = y \log \hat { y } + ( 1 - y ) \log ( 1 - \hat { y } ) $$ 我们希望公式越大越好,反过来,希望 $\log \mathrm { P } ( \mathrm { y } | \mathrm { x } )$ 越小越好,于是得到了最终的 损失函数: $$ L = - [ y \log \hat { y } + ( 1 - y ) \log ( 1 - \hat { y } ) ] $$
上面是 单个样本的损失函数,计算N 个样本,只需要将上面的公式叠加起来。 $$ L = - \sum _ { i = 1 } ^ { N } y ^ { ( i ) } \log \hat { y } ^ { ( i ) } + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - \hat { y } ^ { ( i ) } \right) $$
ok,这个就是交叉熵损失函数完整的推导过程。
自定义损失函数
(1) 继承nn.Module
定义:
|
|
使用:
|
|
(2)自定义函数
注意要所有的数学操作要使用 tensor完成。不需要维护参数,梯度等信息。
|
|
二分类、多分类和多标签问题的区别
二分类、多分类与多标签分类问题使用不同的激活函数和损失函数。
基本概念
二分类:判别这个水果是苹果还是香蕉。 多分类:对于一堆水果,辨别是苹果、梨还是橘子。一个样本只能有一个标签。 多标签分类: 给每一个样本一系列的目标标签。比如一个文档有不同的相关话题,需要加上不同的tag 如宗教、政治和教育。
多分类问题常常是可以转换成二分类问题进行处理的,常见有两种策略。
一对一的策略 给定数据集D这里有N个类别,这种情况下就是将这些类别两两配对,从而产生 $\frac{N*(N-1)}{2}$个二分类任务,在测试的时候把样本交给这些分类器,然后进行投票。
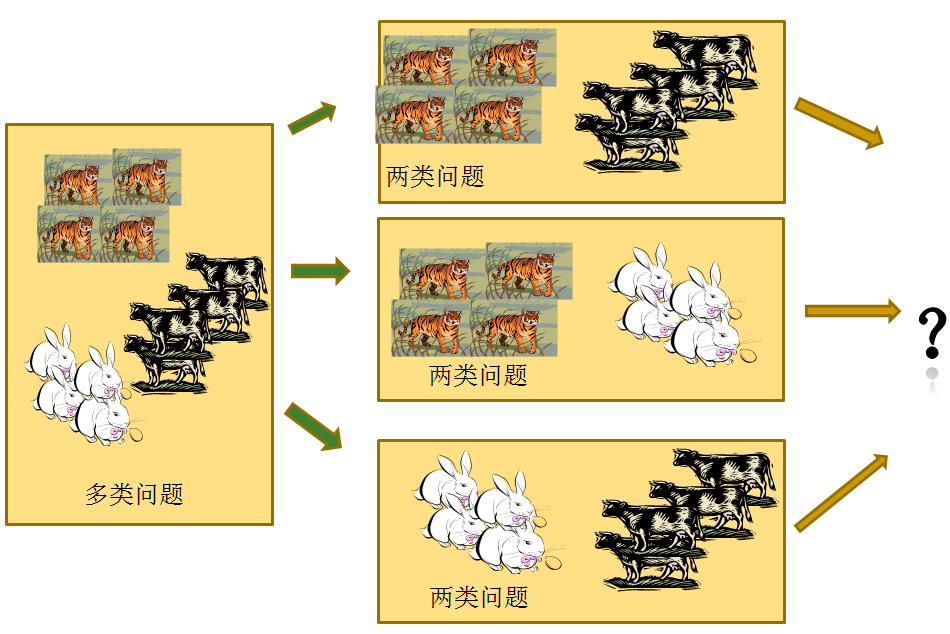
一对其余策略 将每一次的一个类作为正例,其余作为反例,总共训练N个分类器。测试的时候若仅有一个分类器预测为正的类别则对应的类别标记作为最终分类结果,若有多个分类器预测为正类,则选择置信度最大的类别作为最终分类结果。
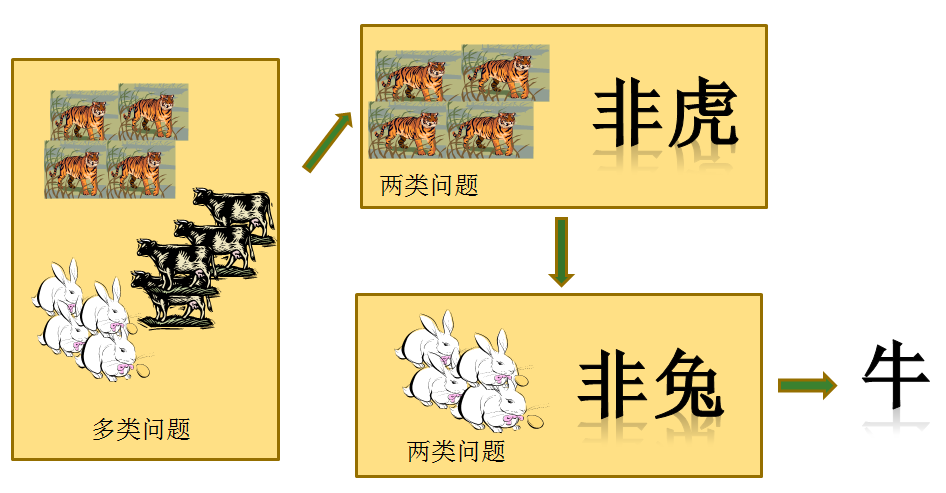
同样,多标签分类和二分类问题也是有关系的。
面临的问题: 图片的标签数目不是固定的,有的有一个标签,有的有两个标签,但标签的种类总数是固定的,比如为5类。
解决该问题: 采用了标签补齐的方法,即缺失的标签全部使用0标记,这意味着,不再使用one-hot编码。例如:标签为:-1,1,1,-1,1 ;-1表示该类标签没有,1表示该类标签存在。
如何衡量损失?
计算出一张图片各个标签的损失,然后取平均值。
如何计算精度
计算出一张图片各个标签的精度,然后取平均值。
该处理方法的本质:把一个多标签问题,转化为了在每个标签上的二分类问题。
损失函数的选择
基于逻辑回归的二分类问题: 使用逻辑回归二分类loss function的推导,上面的一小节是有详细的介绍的。
基于 Softmax 的多分类问题
softmax层中的softmax 函数是logistic函数在多分类问题上的推广,它将一个N维的实数向量压缩成一个满足特定条件的N维实数向。压缩后的向量满足两个条件:
- 向量中的每个元素的大小都在[0,1]
- 向量所有元素的和为 1
因此,softmax适用于多分类问题中对每一个类别的概率判断,softmax的函数公式如下: $$ a _ { j } ^ { L } = \frac { e ^ { z _ { j } ^ { L } } } { \sum _ { k } e ^ { z _ { k } ^ { L } } } $$
基于 Softmax 的多分类问题采用的是 log似然代价函数(log-likelihood cost function)来解决。 单个样本的 log似然代价函数的公式为: $$ C = - \sum _ { i } \left( y _ { i } \log a _ { i } \right) $$ 其中, $y_i $表示标签向量的第 i 个分量。因为往往只有一个分量为 1 其余的分量都为 0,所以可以去掉损失函数中的求和符号,化简为,
$$ C = - \ln a _ { j } $$ 其中,$ a_j $是向量 y 中取值为 1 对应的第 j 个分量的值。
$$
\begin{split}
\operatorname { cost } \left( h _ { \theta } ( x ) , y \right) &= - y _ { i } \log \left( h _ { \theta } ( x ) \right) - \left( 1 - y _ { i } \right) \log \left( 1 - h _ { \theta } ( x ) \right)$ \\
C &= - \sum _ { i } \left( y _ { i } \log a _ { i } \right)$\\
\end{split}
$$
理论上都是使用多类交叉熵函数,但是在实现的时候,深度学习工具keras 是支持两种形式,针对于标签y 的形式,一种是 sparse 一种是 dense分别对应的是 one-hot 形式和 label 的形式。
因为这两个交叉熵损失函数对应不同的最后一层的输出。第一个对应的最后一层是 sigmoid,用于二分类问题,第二个对应的最后一层是 softmax,用于多分类问题。但是它们的本质是一样的,请看下面的分析。
可以看一下交叉熵函数的定义:
$$ -\int p ( x ) \log g ( x ) d x $$
交叉熵是用来描述两个分布的距离的,神经网络训练的目的就是使 $g(x)$ 逼近$ p(x)$。
sigmoid 激活函数和 softmax 激活函数使用场景和区别?
If we want to have a classifier to solve a problem with more than one right answer, the Sigmoid Function is the right choice. We should apply this function to each element of the raw output independently. The return value of Sigmoid Function is mostly in the range of values between 0 and 1 or -1 and 1.
这点明显说的就是 multi-label 的特性
The Softmax Activation Function, also know as SoftArgMax or Normalized Exponential Function is a fascinating activation function that takes vectors of real numbers as inputs, and normalizes them into a probability distribution proportional to the exponentials of the input numbers. Before applying, some input data could be negative or greater than 1. Also, they might not sum up to 1. After applying Softmax, each element will be in the range of 0 to 1, and the elements will add up to 1. This way, they can be interpreted as a probability distribution.
将原来可能存在负数的数字转换成 0-1 的数字,这个就是 softmax 数学上的功能。出来的数值可以被解读成概率分布。
sigmoid is used when you want the output to be ranging from 0 to 1, but need not sum to 1.
Softmax is used for *multi-classification in the Logistic Regression model*, whereas Sigmoid is used for *binary classification in the Logistic Regression model.*
这点是我调研的目的,是否 softmax 可以在二分类中取代 sigmoid 函数?
softmax 和 sigmoid 区别
This is similar to the Sigmoid function. The difference is that, in the denominator, we sum together all of the values. To explain this further, when calculating the value of Softmax on a single raw output, we can’t just look at one element alone, but instead, we have to take into account all the output data.
从数学表达角度看,softmax 是考虑到了整体的信息,sigmoid 只是考虑当下的数值。
sigmoid looks at each raw output value separately.
In the case of softmax, if we want to increase the likehood of one class, the other has to decrease by an equal amount.
softmax 和sigmoid 的联系
Softmax is kind of multi-class sigmoid, but the sum of all softmax units are supposed to be 1. In sigmoid it’s not really necessary.
softmax (join distribution and a multinomial likelihood) 联合分布和多项分布(二项分布的扩展)
sigmoid (marginal distribution and a Bernouli likehood)
Digging deep, in the case of softmax, increasing the output of one class makes the others go down. So sigmoids can probably be preferred over softmax when you outputs are indepentent of one another. To put it more simple, if there are multiple classes and each input can belong to exactly one class, then it makes sense to use softmax, in the other cases, sigmoid seems better.
one more thing is, people use ReLu activations these days (in the hidden layers) and using sigmoid blows up Relu apperently, might be one of the reason why people prefer softmax.
We convert a classifier’s raw output values into probabilities using either a sigmoid function or a softmax function.
simoid 和 softmax 都可以得到概率。
summary
If your model’s output classes are NOT mutualy exclusive and you can choose many of them at the same time, use a sigmoid function on the network’s raw outputs
相反,使用 softmax。
例子
多分类 和多 label 的区别【完成】
The difference between classes and labels is that classes are mutually exclusive and labels are not.
It basically means that an instance can belong to only one class, but can have multiple labels.
查看代码:http://47.94.35.231:8090/tree/notebook/image_tagger
对于本文开始提到的俗语:“CE用于多分类, BCE适用于二分类”其实大部分都是正确的,唯一有待商榷的部分在于多分类(单标签)其实也可以使用BCE,而对于multi-label的多分类,则不能使用CE。
multi-label由于假设每个标签的输出是相互独立的,因此常用配置是sigmoid+BCE, 其中每个类别输出对应一个sigmoid。如果读者仔细看了前面两个小节,相信不用分析,也可以自行得出结果,即这种场景下使用CE将难以收敛,原因跟2.1中的分析类似—我们只计算了某个类别标签为1时的loss及梯度,而忽略了为0时的loss,而每个输出又相互独立,不像softmax函数那样有归一化的限制。所以multi-label是一定不能使用CE作为loss函数的。
https://zhuanlan.zhihu.com/p/48078990
在 multi-label 中损失函数使用的是 BCE 。
|
|
总结
| 分类问题名称 | 输出层使用激活函数 | 对应的损失函数 |
|---|---|---|
| 二分类 | sigmoid | 二分类交叉熵损失函数(binary_crossentropy) |
| 多分类 | softmax | 多类别交叉熵损失函数(categorical_crossentropy) |
| 多标签分类 | sigmoid函数 | 二分类交叉熵损失函数(binary_crossentropy) |
文章作者 jijeng
上次更新 2019-11-28