lstm学习笔记

从 RNN到LSTM，重点介绍LSTM 的网络结构和LSTM是如何缓解RNN 中出现的梯度消失。

循环神经网络(RNN)

一个RNN可以看作是同一个网络的多份副本，每一份都将信息传递到下一个副本。如果我们将环展开的话：

这种链式结构展示了RNN与序列和列表的密切关系。RNN的这种结构能够非常自然地使用这类数据。

RNN 的主要应用如下：

文本相关。主要应用在自然语言处理方面（NLP）、对话系统、情感分析、机器翻译
时序相关。就是在做时序预测问题，比如预测天气、温度，包括有很多人使用其在做预测股票价格的问题

长期依赖(Long Term Dependencies)的问题

对于RNN 来说，可以处理非常短的文本序列（比如下文第一种情况）但是不可以处理比较长的序列（比如下文第二种情况）

有时候，我们只需要看最近的信息，就可以完成当前的任务。比如，考虑一个语言模型，通过前面的单词来预测接下来的单词。如果我们想预测句子“the clouds are in the sky”中的最后一个单词，我们不需要更多的上下文信息——很明显下一个单词应该是sky。 RNN 是可以被用来进行这样问题的训练学习。

然而，有时候我们需要更多的上下文信息。比如，我们想预测句子“I grew up in France… I speak fluent French”中的最后一个单词。不幸的是，随着距离的增大，RNN对于如何将这样的信息连接起来无能为力。

LSTM缓解梯度消失

（1） RNN 中为什么会出现梯度消失

RNN 中的传播公式 $$ \begin{equation} \begin{array}{l}{s_{t}=\phi\left(U x_{t}+W s_{t-1}\right) } \\
{o_{t}=f\left(V s_{t}\right) } \end{array} \end{equation} $$

其中 $s_t$表示隐藏层的状态值，$W$ 表示$s$的权重矩阵， $U$ 表示 $x$的权重矩阵。第一个公式是隐藏层的计算公式，第二层是输出层的计算。

假设时间序列 $t =3$，那么可得到： $t=1$的时候的状态和输出， $$ \begin{equation} \begin{array}{l}{s_{1}=\phi\left(U x_{1}+W s_{0}\right) } \\
o_{1}=f\left(V \phi\left(V x_{1}+W s_{0}\right)\right. \end{array} \end{equation} $$

当 $t =2$ 的状态和输出：
$$ \begin{equation} \begin{array}{l}{s_{2}=\phi\left(U x_{2}+W s_{1}\right)} \\
{o_{2}=f\left(V \phi\left(V x_{2}+W s_{1}\right)\right)=f\left(V \phi\left(V x_{2}+W \phi\left(U x_{1}+W s_{0}\right)\right)\right)}\end{array} \end{equation} $$

当 $t =3$的状态和输出： $$ \begin{equation} \begin{array} {l}{s_{3}=\phi\left(U x_{3}+W s_{2}\right)} \\
o_{3}=f\left(V \phi\left(U x_{3}+W s_{2}\right)\right)=\ldots=f\left(V \phi\left(U x_{3}+W \phi\left(U x_{2}+W \phi\left(U x_{1}+W s_{0}\right)\right)\right)\right) \end{array} \end{equation} $$

所以对于RNN 而言，所谓的无法解决长依赖是因为 $s_0$， $x_1$经过了太多的激活层和权重相乘。而常见的激活函数sigmoid 或者tanh其最大值是1，不可能是一直是1，那么很容易等于0。如 $0.8^{50}=0.00001427247$。这就是RNN 中出现梯度消失的原因。

使用Relu 是可以解决梯度消失，因为 $x>0$ 情况下梯度恒为0。但是容易发生梯度爆炸（虽然可以通过设置适当的阈值）。

如果说通过修改网络结构来解决梯度消失或者梯度爆炸，那么就是LSTM 了。

（2）LSTM 是如何缓解梯度消失的？

$$ \begin{equation} h_{t}=o_{t} \odot \phi \left(f_{t} \odot c_{t-1}+i_{t} \odot \phi \left(W_{x c} x_{t}+W_{h c} h_{t-1}+b_{c}\right)\right) \end{equation} $$

在隐藏层中 LSTM 相对于普通的RNN 有了很多加和，从而保证了在$c$(context) 这个路径上是有梯度的。但是其他路径上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。梯度爆炸相对于梯度消失是更容易解决的。

参考文献 Understanding LSTM Networks

LSTM

LSTM 是用来解决RNN 中的梯度消失/ 梯度爆炸问题的，可以处理 long-term sequence了。

门（gate ）定义： gate 实际上就是一层全连接层，输入是一个向量，输出是一个 0到1 之间的实数向量。公式如下： $$ g ( \mathbf { x } ) = \sigma ( W \mathbf { x } + \mathbf { b } ) $$

遗忘门（forget gate）它决定了上一时刻的单元状态 $c_{t-1} $有多少保留到当前时刻$ c_t$ 输入门（input gate）它决定了当前时刻网络的输入 $x_t$ 有多少保存到单元状态 $c_t$ 输出门（output gate）控制单元状态$ c_t $有多少输出到 LSTM 的当前输出值 $h_t$

（1）LSTM网络

在普通的RNN中，重复模块结构非常简单，例如只有一个tanh层。

LSTM也有这种链状结构，不过其重复模块的结构不同。LSTM的重复模块中有4个神经网络层，并且他们之间的交互非常特别。

（2）LSTM分步详解

LSTM的第一步是决定我们将要从元胞状态中扔掉哪些信息。遗忘门观察$h_{t−1}$和 $x_t$，对于元胞状态 $C_{t−1} $中的每一个元素，输出一个0-1之间的数。1表示“完全保留该信息”，0表示“完全丢弃该信息”。

下一步是决定我们将会把哪些新信息存储到元胞状态中。这步分为两部分。首先，有一个叫做“输入门(Input Gate)”的Sigmoid层决定我们要更新哪些信息。接下来，一个tanh层创造了一个新的候选值，$\tilde { C } _ { t }$，该值可能被加入到元胞状态中。在下一步中，我们将会把这两个值组合起来用于更新元胞状态。

现在我们该更新旧元胞状态 $C_{t−1} $到新状态 $C_t$了。上面的步骤中已经决定了该怎么做，这一步我们只需要实际执行即可。

最后，我们需要决定最终的输出。输出将会基于目前的元胞状态，并且会加入一些过滤。首先我们建立一个Sigmoid层的输出门(Output Gate)，来决定我们将输出元胞的哪些部分。然后我们将元胞状态通过tanh之后（使得输出值在-1到1之间），与输出门相乘，这样我们只会输出我们想输出的部分。

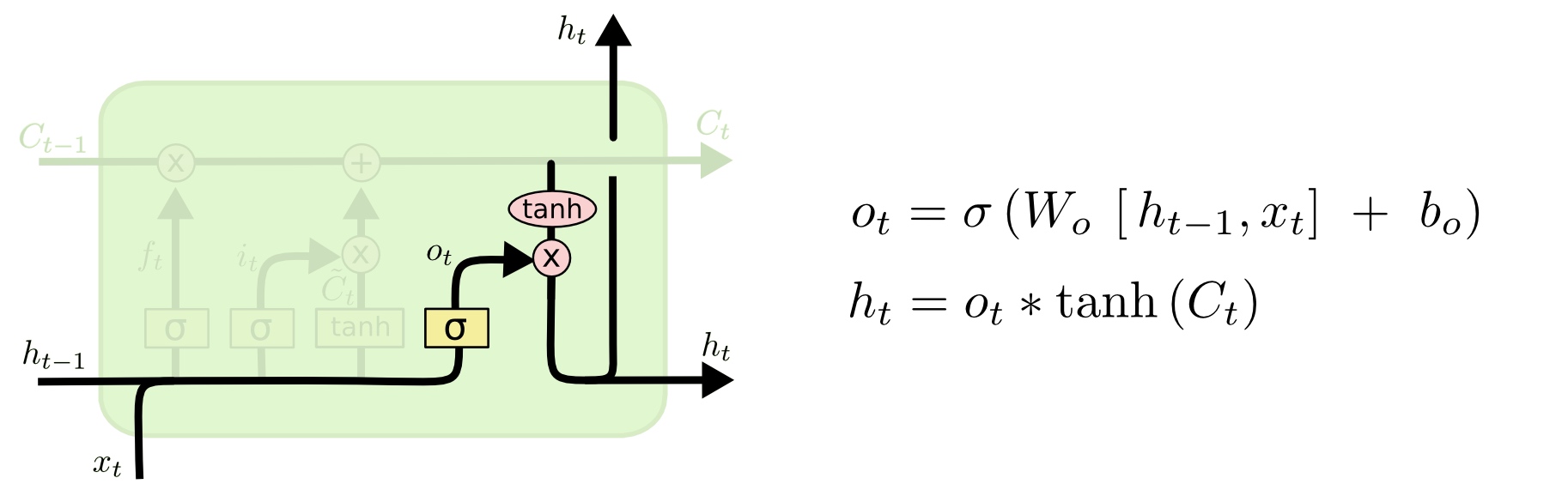
优点：解决了RNN 中的梯度消失的问题，可以处理长依赖

缺点：计算复杂度高，运行时间长

（3）LSTM中参数的计算

首先参数的个数和时间steps 无关
$h_t$ 和 $c_t$ 的维度是相同的
总共四组 [w, b] 参数

直接给出公式 $$ 4(n(m +n) +n)$$ 其中 $m$ 表示输入 $x$ 的维度， $n$ 表示 hidden 或者说 context 的维度。 $(m+n)$ 表示在处理下一层的输入时候，把当前层数据 $x$ 的维度 $m$ 和 hidden 中维度 $n$ 给链接起来，具体可以看一下 lstm 中的示意图。

LSTM参数计算的例子

根据代码可以加深一下理解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


import torch.nn as nn
import torch
from torch.autograd import Variable

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, cell_size, output_size):
        super(LSTM, self).__init__()
        self.hidden_size = hidden_size
        self.cell_size = cell_size
        self.gate = nn.Linear(input_size + hidden_size, cell_size)
        self.output = nn.Linear(hidden_size, output_size)
        self.sigmoid = nn.Sigmoid()
        self.tanh = nn.Tanh()
        self.softmax = nn.LogSoftmax()

    def forward(self, input, hidden, cell):
        combined = torch.cat((input, hidden), 1)
        f_gate = self.gate(combined)
        i_gate = self.gate(combined)
        o_gate = self.gate(combined)
        f_gate = self.sigmoid(f_gate)
        i_gate = self.sigmoid(i_gate)
        o_gate = self.sigmoid(o_gate)
        cell_helper = self.gate(combined)
        cell_helper = self.tanh(cell_helper)
        cell = torch.add(torch.mul(cell, f_gate), torch.mul(cell_helper, i_gate))
        hidden = torch.mul(self.tanh(cell), o_gate)
        output = self.output(hidden)
        output = self.softmax(output)
        return output, hidden, cell

    def initHidden(self):
        return Variable(torch.zeros(1, self.hidden_size))

    def initCell(self):
        return Variable(torch.zeros(1, self.cell_size))

这个对于 pytorch 中 lstm 的实现讲解的比较好：LSTM:Pytorch实现，可以作为参考。

GRU

GRU (gated recurrent unit) 是对于 LSTM 速度上的提升，但是相应的表达能力也受到了限制

GRU 中一共有两个门。GRU 把LSTM 中遗忘门(forget gate) 和输入门(input gate) 使用更新门(update gate) 进行代替。还有一个重置门(reset gate)，重置门主要决定了多少过去的信息需要遗忘。GRU 不会保存内部记忆 context，而且没有输出门。

文章目录

循环神经网络(RNN)

LSTM

GRU