Optimizer
文章目录
深度学习中优化器 （optimizer）讲解。根据学习率的情况分成三个阶段，基础版本Gradient Descent，然后是人工设置学习率阶段和自适应学习率阶段。最后对应pytorch，说明常用的几种学习率优化策略。
vanilla
(1 ) Gradient Descent
针对整个数据集
$$ \theta = \theta - \eta \cdot \nabla _ { \theta } J ( \theta ) $$ 特点：
- 使用整个数据集计算梯度，计算起来非常慢
- 能够找到全局最优点
(2 ) Stochastic Gradient Descent (SGD)
SGD 又走入了另外一个极端，SGD 拿到一个数据之后，马上计算梯度，然后对参数进行更新.
$$ \theta = \theta - \eta \cdot J \left( \theta ; x ^ { ( i ) } , y ^ { ( i ) } \right) $$
特点：
- 无法使用矩阵加速运算
- 收敛速度快
(3) Mini-Batch Gradient Descent （MBGD）
Mini-batch 的方法是在上述两个方法中取了个折衷，每次从全部的熟练数据中取一个 mini-batch 的数据计算。
$$ \theta = \theta - \eta \cdot J \left( \theta ; x ^ { ( i : i + n ) } , y ^ { ( i : i + n ) } \right) $$
batch size 的选择 n： 一般取值在 50～256
目前，mini-batch 的方法是深度学习中主流方法，各种深度学习工具默认也是这种方法。也可以把上述两种方法看成是 mini-batch 的特例，Batch 的方法，就是 mini-batch size 是整个数据集，SGD 方法就是 min-batch=1 的情况.
目前遇到的问题
- learning rate 如何进行自动调整
- 如何跳出马鞍点
在pytorch中的实现：
|
|
功能： pytorch中实现的是带有动量优化的SGD，其中常见的参数：
- params (iterable) 待优化的参数或者定义了参数组的dict
- lr (float) 学习率
- momentum (float 可选) -动量因子，默认是0
- weight_decay (float, 可选) -权重衰减（L2 惩罚），默认是0
注意：pytorch中的使用SGD 和其他的框架不同，pytorch 中是这样的：
$$
\begin{split}
v &= \rho * v+g \\
p &= p- lr * v \\
& = p- lr * \rho * v- lr * g
\end{split}
$$
而其他的框架是
$$
\begin{split}
v &=\rho * v+ lr * g \\
p &=p- v=p- \rho * v- lr * g
\end{split}
$$
其中 $\rho$ 是动量， $v$ 是速度， $g$ 是梯度， pytorch中将 $ \rho * v $这一项也是乘以了一个学习率。
人工设置学习率
- Momentum (heavy-ball method)
$$ x_{t+1}=x_{t}-\alpha \nabla f\left(x_{t}\right)+\mu\left(x_{t}-x_{t-1}\right), \quad \mu \in[0,1], \alpha>0 $$
其中 $\mu$ 是动量因子，取值 0.9 左右。
优点：
- 可以加速 SGD， 并且抑制震荡
缺点：
- Lessard et al. 发现对于简单的凸函数 $f(x)$ ，momentum 不能收敛，课件里给出了一个bad case
- Nesterov Accelerated Gradient
对于上面 momentum出现的bad case， Nesterov 来背锅。
$$ x_{t+1}=x_{t}+\mu\left(x_{t}-x_{t-1}\right)-\gamma \nabla f\left(x_{t}+\mu\left(x_{t}-x_{t-1}\right)\right) $$ 其中学习率$\gamma$, momentum系数$\mu$ 和参数的初始化$x_0$（公式中没有显示出来）
两者的区别，一切尽在图中。（相同的颜色表示相同含义）
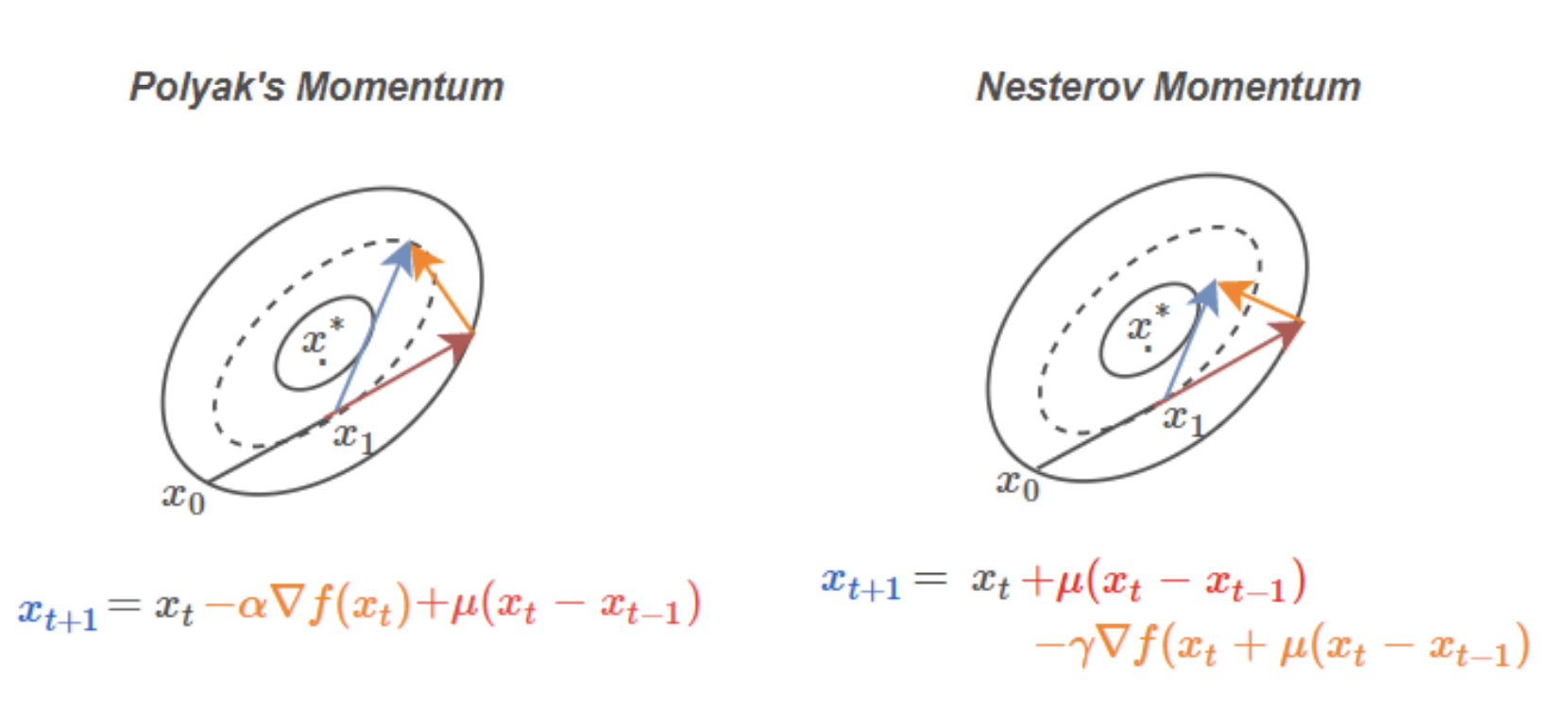Nesterov Accelerated Gradient的关键在于计算梯度之前加上了之前积累的梯度。Notice how the gradient step with Polyak’s momentum is always perpendicular to the level set. taken from here
两种的相同点：都是基于momentum的 optim，都是针对凸优化函数；不同点：momentum 对于简单强凸优化函数，比如导数是二次方的函数，可能出现bad case；相对于而言，Nesterov Accelerated Gradient在凸优化函数中适用性更广。
自适应学习率方法
- Adagrad （Adaptive gradient algorithm）
intuition：自动调节学习率。
$$
\begin{split}
n_{t} &=n_{t-1}+g_{t}^{2} \\
\Delta \theta_{t} &=-\frac{\eta}{\sqrt{n_{t}+\epsilon}} * g_{t}
\end{split}
$$
其中 $n_t$表示从1到$t$ 形成的一个递推项，作为一个约束项， $\epsilon$ 用来保证分母非0，一般取 $1e-8$.实验表明，如果没有进行平方根操作，那么效果很差。
特点：
- 不用人工去tune 学习率，但是仍然需要在开始时候，给定一个学习率（依赖全局初始化学习率）
- 每次增加的嗾使一个正数（平方和），所以训练的中后期，学习率有可能变得非常小（缺点）
实际的使用效果：这个学习率的变化会受到梯度的大小和迭代次数的影响。梯度越大，学习率越小；梯度越小，学习率越大。对于稀疏数据集，效果很好。比如说在RNN 中训练词向量的过程，经常使用到。
- Adadelta
intuition：
- 解决使用Adagrad训练中后期，梯度可能为0 的问题
- 不依赖于初始化的learning rate
首先处理第一个问题：梯度为0. 不使用之前全部的梯度平方和，使用部分。这个时候一种是暴力的滑动窗口的相反，但是作者使用另一种方法： decaying。 $$ E[g ^2] _t=\gamma E[ g ^2] _{t-1}+(1-\gamma) g _t ^2 $$ 其中 $\gamma$ 是类似momentum中的超参数，大概在 0.9左右。
第二个问题是初始化学习率问题。定义了另一个decay 系数，只不过这个是应用在参数 $\theta$ 上的，而不是上面的 $g_t$上。
$$ E[\Delta \theta ^2] _t=\gamma E[\Delta \theta ^2 ] _{t-1}+(1-\gamma) \Delta \theta _t ^2 $$
然后是常用的平方根操作： $$ R M S[\Delta \theta] _t=\sqrt{E [\Delta \theta ^2 ] _t+\epsilon} $$
所以将上述两个方面的更新整合起来：
$$
\begin{split}
\Delta \theta _t &=-\frac{R M S[\Delta \theta] _{t-1}}{R M S[g] _{t}} g _t \\
\theta _{t+1} &=\theta _{t}+\Delta \theta _t
\end{split}
$$
特点：不用设置全局的学习率，学习率是随着迭代次数变化的
- RMSprop
RMSprop是 Geoff Hinton 在其课程中讲到的一种方法。intuition 也是为了解决 Adagrad 中的出现的梯度为0. 实际上 RMSprop 就是 Adadelta 中的第一个方面的公式。
$$
\begin{split}
E[g ^2] _t &=\gamma E[ g ^2] _{t-1}+(1-\gamma) g _t ^2 \\
\theta _{t+1} &= \theta _t-\frac{\eta}{\sqrt{E\left[g^{2}\right] _{t}+\epsilon}} g _{t}
\end{split}
$$
其中 Hinton推荐超参数 $\gamma =0.9$， $\epsilon =0.001$。（ps RMSprop 和 Adadelta解决的方案叫做： exponentially decaying average of past squared gradients）
特点：解决了 Adagrad 中出现的梯度为0的情况
|
|
参数：
- params (iterable) 待优化参数的iterable 或者是低你够了参数组的dict
- lr (float, 可选) 学习率 (默认是 1e-2)
- momentum （float, 可选）动量因子（默认是 0）
- alpha (float, 可选) 平滑因子（默认是 0.99）
- eps (float，可选) 分母中的数值，可以增加数值的稳定性（默认是 1e-8）
- weight_decay (float, 可选) 权重衰减(L2 惩罚) （默认是 0）
alpha：同样也称为学习率或步长因子，它控制了权重的更新比率（如0.001）.较大的值（如0.3）在学习率更新前会更快的初始学习，而较小的值（如1E-5）会令训练收敛到更好的性能
beta1：一阶矩估计的指数衰减率（如0.9）
beta2：二阶矩估计的指数衰减率（如0.99）.该超参数在系数梯度（如在NLP或计算机视觉任务中）中应该设置接近1的数
epsilon：该参数是非常小的数，其为了防止在实现中除以零（如1E-8）
- Adam：Adaptive Moment Estimation
intuition：如果是momentum机制类似一个 ball running down a slope, 那么 Adam behaves a heavy ball with friction。 这种性质是有利于处理非凸优化问题，可能中间出现了一些平滑的局部最优解。如同Adadelta 和 RMSprop，使用了梯度的二阶导数，如同momentum，使用了梯度的一阶导数，把这两者信息结合起来，就是momentum。
In addition to storing an exponentially decaying average of past squared gradients $v_t$, like Adadelta and RMSprop, Adam also keeps an exponentially decaying average of past gradients $m_t$, similar to momentum.
$$
\begin{split}
m _{t} &=\beta _{1} m _{t-1}+(1-\beta _{1}) g _{t} \\
v _{t} &=\beta _{2} v _{t-1}+(1-\beta _{2}) g _{t} ^{2}
\end{split}
$$
其中 $m_t$和 $v_t$ 分别是对梯度的一阶矩估计 （first moment ，the mean） 和二阶矩估计（the second moment ，the uncentered variance），这个是 Adam名字的由来。实验中发现上述公式在初始化阶段，$m_t$ 和$v_t$都是趋向于0，尤其是当 $\beta_1$ 和$\beta_2$ 解决1的时候。
于是进行了 bias-corrected
$$
\begin{split}
\hat{m} _{t} &=\frac{m _{t}}{1-\beta _{1} ^{t}} \\
\hat{v} _{t} &=\frac{v _{t}}{1-\beta _{2} ^{t}}
\end{split}
$$
最后进行了梯度的更新：
$$
\theta _{t+1}=\theta _{t}-\frac{\eta}{\sqrt{\hat{v} _{t}}+\epsilon} \hat{m} _{t}
$$
作者推荐的超参数 $\beta_1 =0.9$， $\beta_2 =0.999$, $\epsilon =10 ^{-8}$
特点：从实践的角度，Adam是优于上述几种的。所以就不用选择了。
|
|
参数
- params (iterable) 待优化参数的iterable 或者是定义了参数组的dict
- lr (float, 可选) 学习率（默认是 13-3）
- betas （Tuple [float, float], 可选） 用于计算梯度以及梯度平方的运行平均值的系数
- eps (float, 可选) 增加数值稳定性而加到分母中的项
- weight_decay （float， 可选） 权重衰减（L2 惩罚） 默认是 0
Adam 的缺陷：
虽然Adam算法目前成为主流的优化算法，不过在很多领域里（如计算机视觉的对象识别、NLP中的机器翻译）的最佳成果仍然是使用带动量（Momentum）的SGD来获取到的。
修正指数移动均值：最近的几篇论文显示较低的$β_2$（如0.99或0.9）能够获得比默认值0.999更佳的结果，暗示出指数移动均值本身可能也包含了缺陷。
虽然Adam算法在实践中要比RMSProp更加优秀，但同时我们也可以尝试SGD+Nesterov动量作为Adam的替代。即我们通常推荐在深度学习模型中使用Adam算法或SGD+Nesterov动量法。
图例
如果空间中存在鞍点：
如果空间中存在若干和局部最优点：
如果…
learning rate scheduler
While training very large and deep neural networks, the model might overfit very easily. This becomes a larger issue when the dataset is small and simple.
当数据集比较简单的时候，容易出现过拟合。
Let’s say that we observe that the validation loss has not decreased for 5 consecutive epochs. Then there is a very high chance that the model is starting to overfit. In that case, we can start to decrease the learning rate, say, by a factor of 0.5.
基本思路一：当 validation loss 不再下降的时候， learning rate 开始 decrease。
基本思路二：希望初期学习率大一些，使得网络收敛迅速一些，在训练后期学习率小一些，这样网络能够收敛到最优解。
learning rate scheduler 也被称为 learning rate decay（学习率衰减）
固定步长衰减、指数衰减、多步衰减、余弦退火衰减
（1）pytorch 中optim 优化器
参数组（param groups）
optimizer 是通过 param_group 来管理参数组， param_group 中保存了参数组和相应的学习率，动量等。可以针对不同的参数设置不同的学习率。
|
|
（2） pytorch中学习率调整策略
learning rate scheduler
PyTorch提供的学习率调整策略分为三大类，分别是
- 有序调整：等间隔调整(Step)，按需调整学习率(MultiStep)，指数衰减调整(Exponential)和 余弦退火CosineAnnealing。
- 自适应调整：自适应调整学习率 ReduceLROnPlateau。
- 自定义调整：自定义调整学习率 LambdaLR。
有序调整
1). 等间隔（固定步长）调整学习率 StepLR
|
|
参数
- step_size(int) - 学习率下降间隔数，若为 30，则会在 30、 60、 90…个 step 时，将学习率调整为 lr*gamma。
- gamma(float)- 学习率调整倍数，默认为 0.1 倍，即下降 10 倍。
- last_epoch(int)- 上一个 epoch 数，这个变量用来指示学习率是否需要调整。当last_epoch 符合设定的间隔时，就会对学习率进行调整。当为-1 时，学习率设置为初始值。
gamma 越大，那么总的变化越慢。
- 指数衰减调整学习率
需要先定义优化器，然后针对不同的优化器去执行不同的策略（下同）
|
|
参数
- gamma- 学习率调整倍数的底，指数为 epoch，即 gamma**epoch
- ast_epoch(int)- 上一个 epoch 数，这个变量用来指示学习率是否需要调整。当 last_epoch 符合设定的间隔时，就会对学习率进行调整。当为-1 时，学习率设置为初始 值
其中参数 gamma 表示衰减的底数，选择不同的 gamma 数值得到幅度不同的衰减曲线
gamma 越大，那么总的变化越慢。
- 多步长衰减
上述固定步长的衰减可以按照固定的区间长度进行学习率的更新，但有时我们希望不同的区间采用不同的更新频率，或者是有的区间更新学习率，有的区间不更新学习率，这个时候就需要使用 MultiStepLR 来实现冬天区间长度控制
|
|
从图中可以看出，学习率在区间[200， 400]内快速的下降，这就是milestones参数所控制的，在milestones以外的区间学习率始终保持不变。
- 余弦退火衰减
严格来说，余弦退火衰减并不应该算是学习率衰减策略，因为它使得学习率按照周期变化。余弦退火衰减可以分为两类：不带热重启和热重启。前者是按照余弦函数的样子衰减到 0 就停止了。后者还会再次变大。
|
|
其包含的参数和余弦知识一致，参数T_max表示余弦函数周期；eta_min表示学习率的最小值，默认它是0表示学习率至少为正值。确定一个余弦函数需要知道最值和周期，其中周期就是T_max，最值是初试学习率。下图展示了不同周期下的余弦学习率更新曲线：
- LambdaLR
Sets the learning rate of each parameter group to the initial lr times a given function.
learning rate 是根据某个 lambda 函数去变化。
自适应调整
1). 按照指标调整学习率（ ReduceLROnPlateau）
plateau （在一段时期的发展后）稳定期，停滞期
当某指标不再变化（下降或升高），调整学习率，这是非常实用的学习率调整策略。 例如，当验证集的 loss 不再下降时，进行学习率调整；或者监测验证集的 accuracy，当accuracy 不再上升时，则调整学习率。
|
|
- mode(str)- 模式选择，有 min 和 max 两种模式， min 表示当指标不再降低(如监测loss)， max 表示当指标不再升高(如监测 accuracy)。
- factor(float)- 学习率调整倍数(等同于其它方法的 gamma)，即学习率更新为 lr = lr * factor
- patience(int)- 忍受该指标多少个 step 不变化，当忍无可忍时，调整学习率。
- threshold_mode(str)- 选择判断指标是否达最优的模式，有两种模式， rel 和 abs。当 threshold_mode == rel，并且 mode == max 时， dynamic_threshold = best * ( 1 +threshold )；当 threshold_mode == rel，并且 mode == min 时， dynamic_threshold = best * ( 1 -threshold )；当 threshold_mode == abs，并且 mode== max 时， dynamic_threshold = best + threshold ；当 threshold_mode == rel，并且 mode == max 时， dynamic_threshold = best - threshold；
- eps(float)- 学习率衰减的最小值，当学习率变化小于 eps 时，则不调整学习率。
自定义调整
自定义调整学习率 LambdaLR
|
|
- lr_lambda(function or list)- 一个计算学习率调整倍数的函数，输入通常为 step，当有多个参数组时，设为 list.
- last_epoch (int) – 上一个 epoch 数，这个变量用来指示学习率是否需要调整。当 last_epoch 符合设定的间隔时，就会对学习率进行调整。当为-1 时，学习率设置为初始 值。
学习率衰减应该是在 optimizer 更新之后应用，代码写成：
|
|
参考文献
Guide to Pytorch Learning Rate Scheduling
这个比较好，给出了代码、图例和数学表达式。
深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam） An overview of gradient descent optimization algorithms
文章作者 jijeng
上次更新 2019-11-17