常见的排序算法总结
分类和总结
- 根据待排序的数据大小不同,使得排序过程中所涉及的存储器不同,可分为内部排序和外部排序。
- 排序关键字可能出现重复,根据重复关键字的排序情况可分为稳定排序和不稳定排序。冒泡、插入和归并是稳定,在这里提到的其他的几个都是不稳定的。
- 对于内部排序,依据不同的排序原则,可分为插入排序、交换(快速)排序、选择排序、归并排序和计数排序。
- 针对内部排序所需的工作量划分,可分为:简单排序 O(n^2)、先进排序 O(nlogn)和基数排序 O(d*n)。
常见算法的性质总结:
排序算法实现默认都是升序…
插入排序(Insert Sort)
思想:
有序数组+insert one every one time
插入排序的工作方式非常像人们排序一手扑克牌一样。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较,如下图所示:


步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5

c++实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#include<iostream>
#include<string>
#include<vector>
using namespace std;
void insert_sort(vector<int> & nums)
{
int n = nums.size();
for(int i =1; i<n; i++)
{
int tmp =nums[i];
int j =i -1;
// 如果当前的元素比之前的元素小,那么一直是为当前的元素往后挪地方
// 这样写法也是有规律的,好好体会
while(j >=0 && tmp < nums[j])
{
nums[j +1] =nums[j];
j --;
}
nums[j+1] =tmp;
}
}
int main()
{
vector<int> nums ={12, 15, 9, 20, 6, 31, 24};
insert_sort(nums);
for(auto u: nums) cout << u<<" ";
cout << endl;
return 0;
}
|
选择排序(Select Sort)
思想和步骤:
select one every time
简单选择排序是最简单直观的一种算法,基本思想为每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止,简单选择排序是不稳定排序。

分析:
无论什么数据进去都是 $O(n^2)$ 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
python 代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def select_sort(lists):
count =len(lists)
for i in range(0, count):
min =i
for j in range(i+1, count):
if lists[min] >lists[j]:
min =j
lists[min], lists[i] =lists[i], lists[min]
return lists
# test
lists =[1, 23,45, 0,-1]
print(select_sort(lists))
|
冒泡排序(Bubble Sort)
思想:
move smallest one time (假设不减)
一遍排序之后,右边是最大,也就是排好序的。这个规则是以此类推的。
有两种说法
- 从右往左: 最小值被移到了最左边。 【冒泡法】的本意
- 从左往右: 最大值被移到了最右边。 此时其实应该叫 【沉石法】
从左向右 沉石法 图解:

分析:
平均时间复杂度:O(n^2)
最坏空间复杂度: 总共 O(n),需要辅助空间 O(1)
1
2
3
4
5
6
7
8
9
10
11
|
def bubble_sort(lists):
count =len(lists)
for i in range(0, count):
for j in range(i+1, count):
if lists[i]> lists[j]:
lists[i], lists[j] =lists[j], lists[i]
return lists
# test
lists =[1,34,45,0,89]
print(bubble_sort(lists))
|
归并排序(Merge Sort)
思想:
divide-and-conquer +递归
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。

分析:
时间复杂度:$O(nlogn)$
空间复杂度:$O(n)$ ,归并排序需要一个与原数组相同长度的数组做辅助来排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
#include<iostream>
#include<vector>
using namespace std;
vector<int> t;
void merge_sort(vector<int> &arr, int l, int r)
{
if (l >= r) return ;
int mid = l +r >> 1;
merge_sort(arr, l , mid);
merge_sort(arr, mid +1, r);
int i =l, j =mid +1, k =0;
while (i <= mid && j <=r)
if(arr[i] <= arr[j])
t[k ++] = arr[i ++];
else
t[k ++] = arr[j ++];
while(i <=mid)
t[k++] = arr[i ++];
while(j <= r)
t[k ++] = arr[j ++];
// 因为 t 中的元素是从 0 到k 的,arr 是从 l 开始的
for(int i=l,j =0; j<k; )
arr[i ++] =t[j++];
}
int main()
{
//int n ;
//cin >> n;
//vector<int> arr;
//for(int i =0 ; i<n; i++) cin >> arr[i];
vector<int> arr ={3, 2, 4, 99};
int n = 4;
t.resize(n+1);
merge_sort(arr, 0, n -1);
for(int i =0; i< n; i++) cout << arr[i]<< " ";
return 0;
}
|
python 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
def merge_sort(arr, l, r):
if l >= r: return
mid = l +r >>1
merge_sort(arr, l, mid)
merge_sort(arr, mid +1, r)
i, j , k = l, mid +1, 0
t =[0] * (len(arr)+1)
while i <= mid and j <= r:
if arr[i] <= arr[j]:
t[k] = arr[i]
k += 1
i +=1
else:
t[k] = arr[j]
k +=1
j +=1
while i<= mid:
t[k] =arr[i]
i +=1
k +=1
while j <= r:
t[k ] = arr[j]
j +=1
k +=1
#print(t)
m =0
while m <k:
arr[l] = t[m]
l +=1
m +=1
if __name__ =="__main__":
n =int(input())
arr =list( map(int, input().split()))
merge_sort(arr, 0, n -1);
print(arr)
|
快速排序(Quick Sort)
思想:分而治之的思想,关键是 partition 函数,经过一次 partition 函数之后,中轴值 pivot 放到了正确的位置,然后递归处理 pivot 左边和右边的元素。
任意选择一个中轴值 pivot (通常选择a[0]),将比他小的数据放在它的前面,比他大的数字放在它的后面。递归进行。
步骤:
- 从数列中挑出一个基准值。
- 将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面(相同的数可以到任一边);在这个分区退出之后,该基准就处于数列的中间位置。
- 递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。
分析:
快速排序的时间复杂度在最坏情况下是O($N^2$),平均的时间复杂度是O(N*logN),采用的是分治的思想,二叉树的结构。
下面以数列 a={30,40,60,10,20,50} 为例,演示它的快速排序过程(如下图)。 这个是经过一个迭代的结果,每一个迭代,都排好了基准数字的位置。按照同样的方法,对子数列进行递归遍历。最后得到有序数组!

在实现的过程中,key 值的选择 while 的遍历顺序是相关的。如果key =arr[left] 那么第一个while 循环是从right 开始的(从后往前);如果key =arr[right] 那么是从left 进行遍历的。
基于python3 的实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
// 从小到大排序
def quick_sort(arr, l, r ):
if l >r : return
key =arr[l]
left, right =l, r
while l<r:
while l <r and arr[r] >= key: r -=1
arr[l] = arr[r]
while l <r and arr[l] <= key: l +=1
arr[r] = arr[l]
arr[l] =key
quick_sort(arr, left, l -1)
quick_sort(arr, l +1, right)
if __name__ =="__main__":
n =int(input())
arr = list(map(int, input().split()))
quick_sort(arr, 0, n-1)
print(arr)
|
给出两种 C ++ 的代码,发现有两点。
- 分开写之后,可以发现和 下面那个算法题目的关系: 这个基准点就是那个 Kth 的一个参考
- 关于while 条件的分析, 如果是i <=j 那么返回的是j, 如果是 i<j 那么返回的i 作为基准点
关于快速排序的三种写法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
/// 从小到大进行排序
int partition(vector<int> &arr, int l, int r)
{
int key =arr[l];
while(l <r)
{
while(l <r && arr[r] >= key) r --;
arr[l] =arr[r];
while(l <r && arr[l] <= key) l++;
arr[r] =arr[l];
}
arr[l] =key;
return l;
}
#include<iostream>
#include<vector>
using namespace std;
void quick_sort(vector<int> & arr, int l, int r)
{
if(l >r) return ;
int key = arr[l];
int left =l, right =r;
while (l <r)
{
while(l <r && arr[r] >= key) r -=1;
arr[l] = arr[r];
while (l <r && arr[l] <= key) l +=1;
arr[r] =arr[l];
}
arr[l] =key;
quick_sort(arr, left, l -1);
quick_sort(arr, l +1, right);
}
int main()
{
int n;
cin >>n;
vector<int> arr(n);
for(int i =0; i< n; i++)
cin >> arr[i];
quick_sort(arr, 0, n -1);
for(int i =0; i< n; i++) cout << arr[i] << " ";
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include<iostream>
#include<vector>
using namespace std;
// 快排 一般时间复杂度 nlogn ,最坏的时间复杂 n^2,一般很难达到
void quick_sort(vector<int> & arr, int l, int r)
{
if (l >r) return ;
int left =l, right =r;
int key =arr[l];
while(l <r)
{
while(l <r && arr[r] >= key) r -=1;
arr[l] =arr[r];
while(l< r && arr[l] <= key) l +=1;
arr[r] =arr[l];
}
arr[l] =key;
quick_sort(arr, left, l-1);
quick_sort(arr, l+1, right);
}
int main()
{
vector<int> arr;
int n;
cin >>n;
for(int i =0; i<n; i++)
{
int tmp;
cin>> tmp;
arr.push_back(tmp);
}
quick_sort(arr, 0, arr.size() -1);
for(auto u: arr)
cout << u<<" ";
cout <<endl;
return 0;
}
|
Kth Largest Element in an Array
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
Tips: 使用的是 快排的思想,最后的平均时间复杂度是O(N) ,所以是一个不错的算法。 kth 和 ”快排“ 实现的时候稍微有一些区别,前者只有发现 一组数据(一个比pivot 大,一个比 pivot 小)才进行交换,后者是是 两个while, 只要发现一个就进行交换。这个是细微的差别。求解K 最大,那么数组适合的是降序,求解K 最小,那么数组适合升序。关键这个求解的是 K 最大或者最小,那么是不需要整个数组是有序的,而是找出某个数字是,即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution(object):
def partition(self, l, r, nums):
# 快排的思路
key =nums[r]
while l<r:
while l <r and nums[l] >= key: l +=1
nums[r] =nums[l]
while l < r and nums[r] <= key : r -=1
nums[l] =nums[r]
nums[r] =key
return l
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
# 使用快排的思路去解题, 最后的时间复杂度是 O(n)
# 题目要求找到第k 个大的即可,不要求数组的其他部分是有序的
l, r =0, len(nums) -1
while True:
pos =self.partition(l, r , nums)
if pos ==k -1:
return nums[pos]
elif pos > k -1:
r = pos -1
else: l =pos +1
return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
#include<iostream>
#include<vector>
using namespace std;
// 时间复杂度是 nlog k
// 注意这里一定要传递的是引用
int partition(vector<int>& arr, int l, int r)
{
int key =arr[r];
while(l <r)
{
while(l <r && arr[l] >= key) l ++;
arr[r] =arr[l];
while(l <r && arr[r] <= key) r --;
arr[l] =arr[r];
}
arr[r] =key;
return l;
}
int find_kth_largest(vector<int>& arr,int n, int k)
{
if(k > n) return -1;
int l =0, r =n -1;
while( true)
{
int pos =partition(arr, l, r);
if( pos ==k -1) return arr[pos];
else if(pos > k -1) r =pos -1; // k-1在小部分,那么r =pos -1
else l =pos +1;
}
}
int partition1(vector<int> & arr, int l, int r)
{
int key =arr[l];
while(l <r)
{
while(l <r && arr[r] >= key) r --;
arr[l] =arr[r];
while(l <r && arr[l] <= key) l ++;
arr[r] =arr[l];
}
arr[l] =key;
return l;
}
int find_kth_smallest(vector<int>& arr, int n, int k)
{
if(k >n ) return -1;
int l =0, r =n -1;
while(true)
{
int pos =partition1(arr, l, r);
if(pos ==k -1) return arr[pos];
else if(pos < k-1) l =pos +1; // 二分的真谛在于一定包含结果区间
else r =pos -1;
}
}
int main()
{
/*
int n, k ;
cin >>n>>k;
vector<int> arr;
for(int i =0; i<n; i++)
{
int tmp;
cin >>tmp;
arr.push_back(tmp);
}
*/
vector<int> arr ={1, 5, 7, 0, 2};
int k =2;
int n =5;
cout <<"result: "<<endl;
cout << find_kth_largest(arr, n, k)<< endl;
cout << find_kth_smallest(arr, n, k)<< endl;
return 0;
}
|
使用内置的函数先sort () 然后选择,那么时间复杂度是 $nlogn$。 如果使用partition() 函数, 就能优化成 $O(n)$. 讲解如下
That’s not quick-sort, that’s quick-select. After partitioning, the the former continues to sort both parts while the latter continues to search only one part. So your costs are like n+n/2+n/4+n/8+… = 2n = O(n) instead of n+2·n/2+4·n/4+… = O(n log n).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include<iostream>
#include<vector>
using namespace std;
int partition(vector<int> & arr, int l, int r)
{
int key =arr[r];
while(l <r)
{
while(l <r && arr[l] >= key) l ++;
arr[r] =arr[l];
while (l <r && arr[r]<= key) r --;
arr[l] = arr[r];
}
return l;
}
int kth_largest(vector<int> arr, int k)
{
if(arr.empty()) return -1;
int l =0,r= arr.size()-1;
if (k >arr.size()) return -1;
while (true) {
int pos =partition(arr, l, r);
if(pos ==k -1) return arr[k];
else if(pos > k-1) r =pos -1;
else l = pos +1;
}
return -1;
}
int main()
{
int n, k;
vector<int> arr;
cin>> n>>k;
arr =vector<int>(n);
for(int i =0; i<n; i++) cin>> arr[i];
cout<< kth_largest(arr, k)<<endl;
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
# Hello World program in Python
# python 中只是支持 +=1 不支持 ++ 操作
def partition(arr, l, r):
key = arr[r]
while l < r:
while l < r and arr[l] >= key:
l +=1
arr[r] = arr[l]
while l < r and arr[r] <= key:
r -=1
arr[l] = arr[r]
arr[r] = key
return l
def findKthLargest(nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
if not nums or k > len(nums): return False;
l, r = 0, len(nums) - 1
while True:
pos = partition(nums, l, r)
if (pos == k - 1):
return nums[pos]
elif (pos > k - 1): r =pos -1
else: l =pos +1
return -1
nums = [1, 2, 3, 4, 5]
k = 2
print(findKthLargest(nums, k))
|
堆排序
堆排序(Heap Sort)的时间复杂度是$O(nlogn) $, 最坏情况下也是如此.而快速排序(Quick Sort), 若初始记录序列有序, 快速排序将退化为起泡排序(Bubble Sort), 时间复杂度是$O(n^2) $.这是堆排序比快速排序的优点.
堆排序可以使用数组实现,
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引是 (2*i);
- 索引为i的左孩子的索引是 (2*i+1);
- 索引为i的父结点的索引是 floor(i/2);
当然也是可以从 0开始计数。在C++ 中使用 标准库函数中的 priority_queue 就可以使用。优先队列。
参看另外一篇博客
使用堆排序的一个问题,求解最小K 个元素。时间复杂度是 $O(nlog k) $.push_up操作时间复杂度O(logk),push_down也是O(logk),总计遍历数据一遍。所以最终复杂度是O(Nlogk)。详细的解释可以看这里 。实现的时候,直接使用库函数了。
堆是一棵顺序存储的完全二叉树,堆排序是一种树形选择排序,其时间复杂度为O(nlogn),空间复杂度:对于记录较少的文件不推荐使用,对于较大的文件还是有效的.堆分为大根堆和小根堆。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。小根堆的要求是每个节点的值都不小于其父节点的值,即A[PARENT[i]] <= A[i]。
堆的每次调整交换堆顶和最后一个元素,然后只是调整堆顶和堆顶的左右孩子树的关系。有建立堆,调整堆和堆排序三个步骤。
这个是讲解视频
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
n,m =tuple(map(int, input().split()))
nums =list(map(int, input().split()))
def heapify( x):
if x>=n : return
cl =2*x+1
cr =cl +1
min_v =x
if(cl <n and nums[min_v] > nums[cl]): min_v =cl
if(cr <n and nums[min_v] > nums[cr]): min_v =cr
if(min_v != x):
nums[min_v], nums[x] =nums[x], nums[min_v]
heapify(min_v)
if __name__ =="__main__":
# build heap
for i in range((n-1)//2, -1, -1):
heapify(i)
# heap sort
while m:
print(str(nums[0])+" ")
nums[0] =nums[n-1]
heapify(0)
n -=1
m -=1
|
使用c++ 实现的是小根堆, heapify , build heap 和heap sort 的操作. 使用数组作为存储的结构,从 1到n 存储,这样第 i 个结点的父节点是 i/2, 左右子节点是 2*i 和2*i+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
// 堆排序的核心思想,保证堆顶元素和左右两个孩子的大小关系; 如果是大根堆,那么就是堆顶元素大于两个孩子的元素
#include<bits/stdc++.h>
using namespace std;
const int N =1e5+11;
int n,m;
int nums[N];
// 这个是小根堆
void heapify(int x)
{
int lc = 2*x, rc =lc+1;
int min_v =x;
if(lc <=n && nums[min_v] > nums[lc] ) min_v =lc;
if(rc <=n && nums[min_v] > nums[rc]) min_v =rc;
if(min_v != x)
{
swap(nums[min_v], nums[x]);
heapify(min_v);
}
}
int main()
{
cin >>n >>m;
for(int i =1; i<=n;i++) scanf("%d", &nums[i]);
// build heap
for(int i =n/2; i; i--)
heapify(i);
// heap sort
while(m --)
{
printf("%d ", nums[1]); // 堆顶元素
nums[1] =nums[n];
heapify(1);
n --;
}
return 0;
}
|
补充:
stack 栈, FILO,先进后出,栈溢出都是它
heap,大根堆、小根堆,常用在大量的数据进行排序,是一种树形结构
queue 队列,先进先出
c++ 和python中都是如何调用的呢?(补充)
桶排序
排序算法分两大类,基于比较的排序和非基于比较的排序。没啥好解释的,基于比较的,比如冒泡排序、插入排序、选择排序、希尔排序、堆排序、归并排序、快速排序,基于比较的排序复杂度下限为 $O(nlogn) $。非基于比较的排序如,桶排序、计数排序、基数排序。非基于比较的排序不受 $O(nlogn) $这个下限的约束,能够达到 $O(n)$的复杂度。但是非基于比较的算法一般对数据有比较严格的要求,所以一般用来处理一些有特征性的数据的排序。
适用范围:
主要适用于小范围整数数据,且独立均匀分布,可以计算的数据量很大,而且符合线性期望时间。
算法步骤:
- 设置固定数量的空桶。
- 把数据放到对应的桶中。
- 对每个不为空的桶中数据进行排序。
- 拼接从不为空的桶中数据,得到结果。

- 设置桶的数量为5个空桶,找到最大值110,最小值7,每个桶的范围20.8=(110-7+1)/5 。
- 遍历原始数据,以链表结构,放到对应的桶中。数字7,桶索引值为0,计算公式为floor((7 – 7) / 20.8), 数字36,桶索引值为1,计算公式floor((36 – 7) / 20.8)。
- 当向同一个索引的桶,第二次插入数据时,判断桶中已存在的数字与新插入数字的大小,按照左到右,从小到大的顺序插入。如:索引为2的桶,在插入63时,桶中已存在4个数字56,59,60,65,则数字63,插入到65的左边。
- 合并非空的桶,按从左到右的顺序合并0,1,2,3,4桶。
- 得到桶排序的结构
实际的应用场景:
一年的全国高考考生人数为500 万,分数使用标准分,最低100 ,最高900 ,没有小数,你把这500 万元素的数组排个序。
拓扑排序
拓扑序列: 设在 $G =(V, E)$ 是一个具有 $n$ 个顶点的有向图,集合 $V$ 的顶点序列 $v_1$, $v_2$… $v_n$ 称为一个拓扑序列,需满足下列条件: 若从顶点 $v_i$ 到$v_j$ 有一条路径,那么在顶点序列中顶点 $v_i$ 必须在顶点 $v_j$ 之前。
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
拓扑排序基本思想:
- 从AOV 网中选择一个没有前驱顶点并且输出
- 从AOV 网中删除该顶点,并且删去所有以该顶点为尾的弧
- 重复上述两部,直到全部顶点都被输出,或者AOV 网中不存在没有前驱的顶点。
拓扑序列不是唯一的哦。
AOV 网: activity on vexes(在顶点上的活动)
** 拓扑排序的应用**
- 判断是否存在环,如果输出能够得到所有的顶点,那么没有存在环;否则就存在环。
- 拓扑排序通常用来“排序” 具有依赖关系的任务。
这里要补充两个概念,偏序和全序?
偏序:有向图中两个顶点之间不存在环路,至于连通与否,是无所谓的。全序:就是在偏序的基础之上,有向无环图中的任意一对顶点还需要有明确的关系(反映在图中,就是单向连通的关系,注意不能双向连通,那就成环了)。 意思就是讲,一个不确定的偏序关系经全序后就有一种确定的先后顺序了。既然有先后,那么在实际生活中的选课问题,比如大一时一定要修完这门课,大二才学第二门课,这种排课问题就是拓扑排序问题。
图的存储结构- 邻接矩阵和邻接表
简单的说,图由表示数据元素的集合V和表示数据之间关系的集合E组成,记为G=<V,E>。图又分为有向图与无向图。下面是图的一些基本元素:
- 边(edge):顶点的序偶。
- 顶点(vertex):数据元素。
- 权重(weight):用来表示一个顶点到另一个顶点的距离、代价、耗费等。
- 度(degree):与该顶点相关联的边的数目,入度、出度等等。
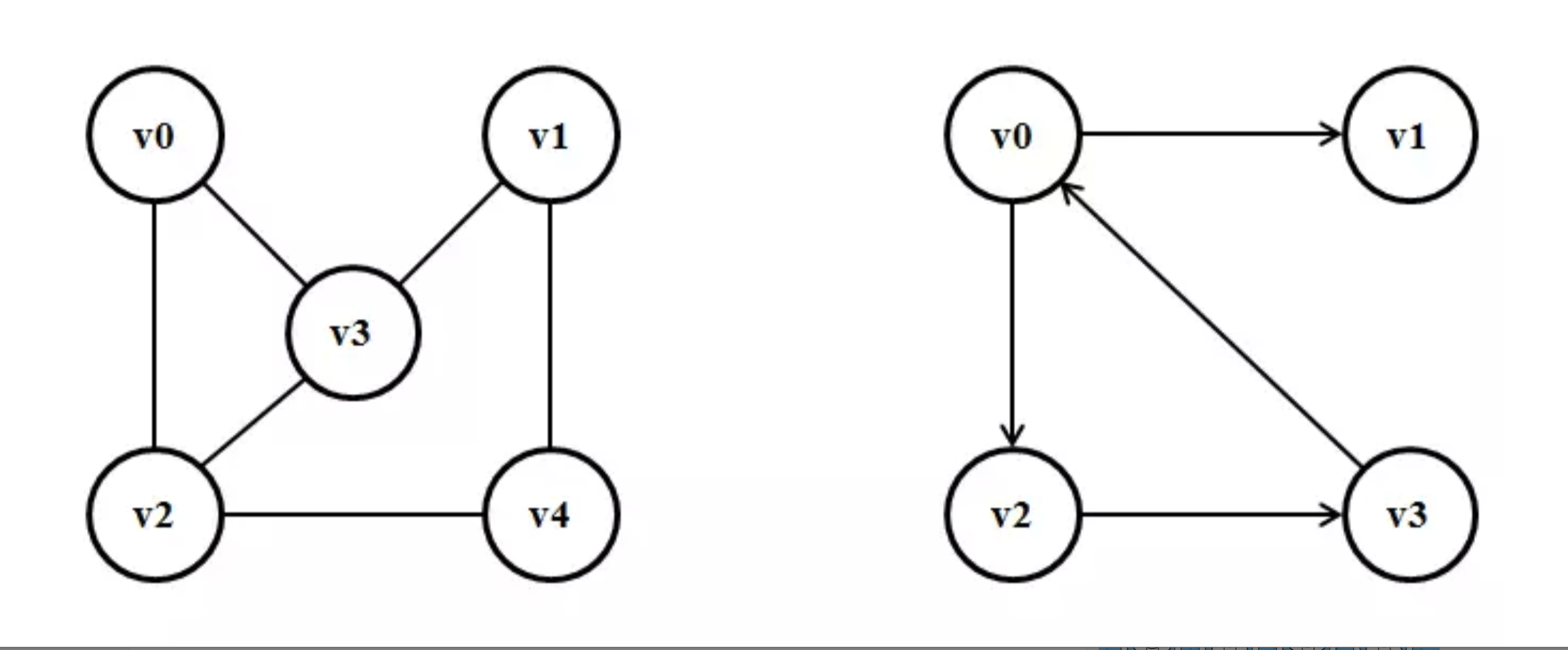
图的相邻矩阵储存类型
图的相邻矩阵或邻接矩阵表示定点之间的邻接关系,即表示顶点之间有边或没有边的情况。如下图则是无向图G1和有向图G2的邻接矩阵。
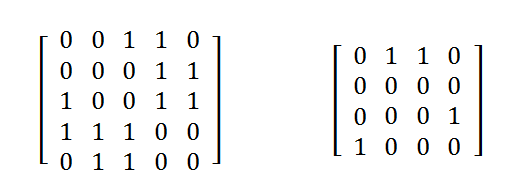
无论是有向图还是无向图,邻接矩阵比较好表示。
有向图的邻接表是比较好表示:
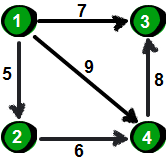 下一个结点是有向图中结点的下一个结点。
下一个结点是有向图中结点的下一个结点。
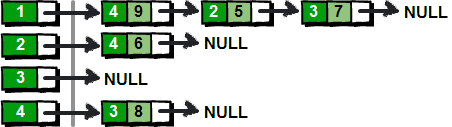
使用邻接表表示无向图
Course Schedule
使用邻接表和队列 (bfs)实现拓扑排序。 时间复杂度是 $ O(n+m)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
bool canFinish(int num, vector<vector<int>>& pre) {
vector<vector<int>> adj(num);
vector<int> in_degree(num, 0);
for(int i =0; i< pre.size() ; i++)
{
in_degree[pre[i][0]] ++;
adj[pre[i][1]].push_back(pre[i][0]);
}
for(auto u: in_degree) cout << u<<" ";
queue<int> q;
int couts =0;
for(int i =0; i< num; i++)
{
if(in_degree[i] ==0) q.push(i);
}
while(!q.empty())
{
int t =q.front();
q.pop();
couts +=1;
for(int i =0; i< adj[t].size(); i++)
{
in_degree[adj[t][i]] --;
if(in_degree[adj[t][i]] ==0) q.push(adj[t][i]);
}
}
return couts ==num;
}
};
|
207. Course Schedule
拓扑排序 ($O(m +n)$)
- 将先修关系构成一张图,由每个数对的第二个数字向第一个数字连边。
- 首先将所有入度为0的点进队,准备拓扑排序。
- 宽搜过程中,将当前结点所关联的结点的入度减1;若发现新的入度为0的结点,则将其进队。
- 最后如果遍历了所有结点,则说明可以满足要求;否则,先修关系存在环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
// 是一个判别题目, 如果说拓扑排序能够排下来,那么就可以认为是达到了要求
bool canFinish(int n, vector<vector<int>>& pre) {
vector<vector<int>> adj(n); // 这个表明可以 adj[i] 这样进行遍历
vector<int> in_degree(n, 0);
queue<int> q;
int counts =0;
// 处理原来的数据变成邻接表和入度表
for(int i =0; i< pre.size() ; i++)
{
adj[pre[i][1]].push_back(pre[i][0]);
in_degree[pre[i][0]] ++;
}
// 这个n 表示的就是课程的数量,判别的是课表的合理与否,所以直接push的i
for(int i =0; i< n ; i++)
if(in_degree[i] ==0) q.push(i);
while(q.size())
{
auto t =q.front();
q.pop();
counts ++;
for(int i =0; i< adj[t].size(); i++)
{
in_degree[adj[t][i]] --;
if(in_degree[adj[t][i]] ==0) q.push(adj[t][i]);
}
}
return counts ==n;
}
};
|
python 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
from queue import Queue
class Solution:
def canFinish(self, n: int, pre: List[List[int]]) -> bool:
adj ={}
in_degrees ={}
# 初始化的操作, 类似实现了一种键值对的关系
for i in range(n):
adj[i] =[]
in_degrees[i] =0
# 赋值语句
'''
for i in range(len(pre)):
adj[pre[i][1]].append(pre[i][0])
in_degrees[pre[i][0] ] +=1
'''
for c, p in pre:
adj[p].append(c)
in_degrees[c] +=1
q = Queue()
# 将所有入度为0 的点,放入到
for i in range(n):
if(in_degrees[i] ==0): q.put(i)
count =0
print(adj)
while q.qsize():
t =q.get()
count +=1
for val in adj[t]:
in_degrees[val] -=1
if(in_degrees[val] ==0): q.put(val)
return n ==count;
|
python3 中使用queue 的常见的操作
1
2
3
4
5
|
python 中使用queue 的常用操作
from queue import *
q = Queue()
q.put(i)
t =q.get()
|
210. Course Schedule II
是第一类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public:
// 使用c++ 实现拓扑排序
vector<int> findOrder(int n, vector<vector<int>>& pre) {
vector<vector<int>> adj(n);
vector<int> in_degree(n, 0);
queue<int> q;
// 初始化
for(int i =0; i< pre.size(); i++)
{
adj[pre[i][1]].push_back(pre[i][0]);
in_degree[pre[i][0]] +=1;
}
// 维护一个队列
for(int i =0; i< n; i++)
if(in_degree[i] ==0) q.push(i);
vector<int> res;
while(q.size())
{
auto t =q.front();
q.pop();
res.push_back(t);
for(int i =0; i< adj[t].size() ; i++)
{
in_degree[adj[t][i]] -=1;
if(in_degree[adj[t][i]] ==0) q.push(adj[t][i]);
}
}
if(res.size() == n) return res;
else return vector<int>{};
}
};
|
python 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution:
# 上一道题目返回的是一个true or false 的问题,这道题目返回的是拓扑排序之后的结果, 使用一个list 存储就好了
def findOrder(self, n: int, pre: List[List[int]]) -> List[int]:
adj ={}
in_degree={}
# 初始化
for i in range(n):
adj[i] =[]
in_degree[i] =0
# 处理pre 的关系
for c, p in pre:
adj[p].append(c)
in_degree[c] +=1
# 初始化queue
from queue import Queue
q =Queue()
for i in range(n):
if(in_degree[i] ==0): q.put(i)
res =[]
while q.qsize():
t =q.get()
res.append(t)
for val in adj[t]:
in_degree[val] -=1
if(in_degree[val] ==0): q.put(val)
return res if len(res) ==n else []
|
- 时间复杂度
排序时间复杂度为 $O(nlogn)$,枚举课程需$ O(n)$,每次访问单调队列需要 $O(logn)$(因为基于 大根堆实现的),故总时间复杂度为 $O(nlogn)$。
- 空间复杂度
$O(n)$
630. Course Schedule III
这种算法更加的精妙,先是无脑的加入,如果有不符合条件的,那么就pop 出来。需要单独记录一个tot 的时间, tot[i]+ lasting > d[i] 的时间,那么就需要弹出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
// 排序算法+使用大根堆
int static cmp(vector<int> & a, vector<int> &b)
{
return a[1] < b[1];
}
int scheduleCourse(vector<vector<int>>& courses) {
// 首先是按照结束时间排序,
sort(courses.begin(), courses.end(), cmp);
// 使用大根堆,保证当每次弹出的时候,弹出的都是持续时间最长的那个
priority_queue<int> max_heap;
int ton =0;
for(int i =0; i< courses.size(); i++)
{
max_heap.push(courses[i][0]);
ton += courses[i][0];
if(ton > courses[i][1])
{
ton -= max_heap.top(); // 这个还是比较有意思的
max_heap.pop();
}
}
return max_heap.size();
}
};
|
python 实现
python 内置的函数实现的是小根堆,那么push 进去的是 -t,这个操作中更加能体现 先是无脑加,如果不符合要求,那么再pop 出来。
多思考使用大根堆和小根堆区别。是要保证pop 出来的是时长最长的那个,因为如果可以的话,尽可能选择时长短的课程呢。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution:
# python 中使用heapq 实现的小根堆
# 如果从逻辑上应该使用大根堆,那么在添加值的时候,应该添加负值
def scheduleCourse(self, courses: List[List[int]]) -> int:
courses.sort(key=lambda x: x[1])
tot =0
min_heap =[]
for l, d in courses:
heapq.heappush(min_heap, -l)
tot += l
if(tot > d):
tot += heapq.heappop(min_heap)
return len(min_heap)
|
小范围(基本有序)排序
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过 $k$,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
给定一个int数组A,同时给定A的大小 $n$和题意中的 $k$,请返回排序后的数组。
测试样例:
[2,1,4,3,6,5,8,7,10,9],10,2
返回:[1,2,3,4,5,6,7,8,9,10]
算法思路:
对前$k$ 个数字简历小根堆,然后对剩下的元素和对进行维护,每次从堆顶弹出就是最小元素,记录出堆顶的序列,最后从小到大的序列。时间复杂度是$klogk + (n-k)*logk $,相对于$n$来说$k$是比较小的,所以最后的时间复杂度可以表示为$nlogk$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include<iostream>
#include<vector>
using namespace std;
// 这里 c++ 和c 进行了混用
void heapify(int * heap, int p, int k)
{
int lc =2*p+1, rc =lc +1; // 如果heap 的存储是从0 开始,那么是要从这样写的
int min_v =p;
if(lc < k && heap[min_v] > heap[lc]) min_v =lc;
if(rc <k && heap[min_v] > heap[rc]) min_v =rc;
if(min_v != p)
{
swap(heap[min_v], heap[p]);
heapify(heap, min_v, k);
}
}
vector<int> sortElement(vector<int> & nums, int n, int k)
{
int heap[k];
for(int i =0; i< k; i++)
heap[i] =nums[i];
for( int i =k /2 -1; i>=0; i--)
heapify(heap, i, k);
for(int i =k; i< n; i++)
{
nums[i-k] =heap[0];
heap[0] = nums[i];
heapify(heap, 0, k);
}
// 对最后k 个元素进行排序
for(int i =n-k; i<n; i ++)
{
nums[i] =heap[0];
swap(heap[k-1], heap[0]); //最后是变小的
heapify(heap, 0, --k);
}
return nums;
}
int main()
{
int n, k;
//cin >>n>>k;
n =10;
k =2;
vector<int> nums ={2, 1, 4,3, 6, 5, 8, 7, 10, 9};
vector<int> res =sortElement(nums, n, k);
for(auto u: res)
cout << u<< " ";
return 0;
}
|
参考文献
1). 算法动图效果
2). 排序算法分类
3). 桶排序算法详解









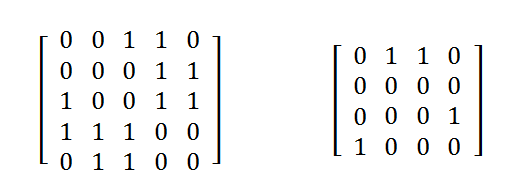
 下一个结点是有向图中结点的下一个结点。
下一个结点是有向图中结点的下一个结点。