并查集是一种树型数据结构，用于处理不相交 (Disjoint Sets) 的合并及查询问题。
定义
并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。
并查集属于一种数据结构算法，一般来说有半确定的模块功能：
- 初始化操作
- 合并操作 （能够体现层级关系的，数量少的集合是需要并入到数量大的集合中去）
- 路径压缩 （在查询的过程中，用进行路径压缩）
对于查找操作，假设需要确定x所在的的集合，也就是确定集合的代表元。判断两个元素是否属于同一集合，只需要看他们的代表元是否相同即可。并查集为了避免时间和空间上的损耗，在每一轮的查找时，都要进行一次路径压缩优化。
** 路径压缩 **： 在递归找到根节点的时候，把当前节点到根节点间所有节点的父节点都设置为根节点。
我们来看下图，首先我们有个这样的一棵树，现在要找到元素9所在树的根节点，在找根节点的过程中使用路径压缩，也就是说9到根的路径上的节点9，6，3，1的父节点都设置成为根节点0，所以呢，在FIND-SET(9)之后，树的形态就变成了下面的样子
我们可以看到经过路径压缩的节点及其子树到根节点的深度减小了很多，所以在以后的操作中，查找根节点的速度会快很多
这样可以将查询一个结点的根节点的时间复杂度从 O(log N) 降到 O(1)
还有一个比较有趣的图解可以说明这个优化：
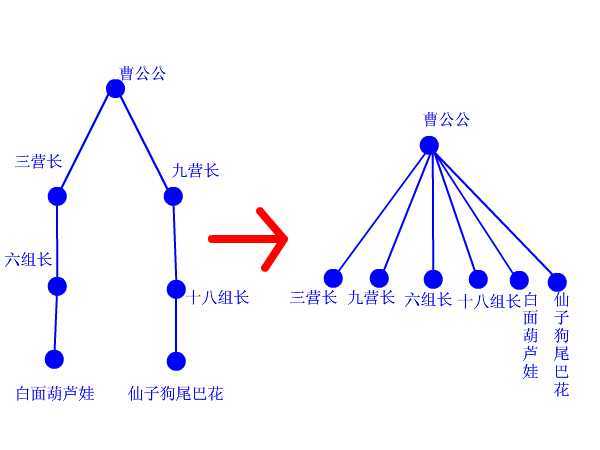
并查集中的两个操作时间复杂度都是 $O(1)$
- 合并两个集合
- 判断两个点是否在同一个集合中
并查集中有两个优化：路径压缩 和按秩合并。加上第一个优化，那么时间复杂度是 $log n$，如果加上第二个优化，那么时间复杂度是 $log log n$
基于C语言的两种实现
基于数组和结构体的两种实现（C 语言），一般来说简单问题使用数组，复杂问题使用结构体。
** 数组 **
初始化
1
2
3
4
5
6
7
8
9
10
11
12
|
#define MAX 10000
int set[max];//集合index的类别，或者用parent表示
int rank[max];//集合index的层次，通常初始化为0
int data[max];//集合index的数据类型
//初始化集合
void Make_Set(int i)
{
set[i]=i;//初始化的时候，一个集合的parent都是这个集合自己的标号。没有跟它同类的集合，那么这个集合的源头只能是自己了。
rank[i]=0;
}
|
查找函数
1
2
3
4
5
6
7
8
9
|
//查找集合i（一个元素是一个集合）的源头（递归实现）
int Find_Set(int i)
{
//如果集合i的父亲是自己，说明自己就是源头，返回自己的标号
if(set[i]==i)
return set[i];
//否则查找集合i的父亲的源头
return Find_Set(set[i]);
}
|
合并函数
1
2
3
4
5
6
7
8
9
10
11
12
|
void Union(int i,int j)
{
i=Find_Set(i);
j=Find_Set(j);
if(i==j) return ;
if(rank[i]>rank[j]) set[j]=i;
else
{
if(rank[i]==rank[j]) rank[j]++;
set[i]=j;
}
}
|
** 结构体实现**
初始化
1
2
3
4
5
6
7
|
struct Node
{
int data;
int rank;
int parent;
}node[MAX];
|
查找函数
1
2
3
4
5
6
7
8
9
10
11
|
/**
*查找集合i（一个元素是一个集合）的源头（递归实现）。
如果集合i的父亲是自己，说明自己就是源头，返回自己的标号；
否则查找集合i的父亲的源头。
**/
int get_parent(int x)
{
if(node[x].parent==x)
return x;
return get_parent(node[x].parent);
}
|
合并函数
1
2
3
4
5
6
7
8
9
10
11
12
13
|
void Union(int a,int b)
{
a=get_parent(a);
b=get_parent(b);
if(node[a].rank>node[b].rank)
node[b].parent=a;
else
{
node[a].parent=b;
if(node[a].rank==node[b].rank)
node[b].rank++;
}
}
|
应该是有三个版本的 union-find 算法的：
|
find() |
union() |
总的时间复杂度 |
| quick-find |
O(1) |
O(N) |
O(M*N) |
| quick-union |
O(logN ~ N) |
O(1) |
O(M*N) 极端 |
| WeightedUF |
O(log N) |
O(N) |
O(M *log N) |
这里有三个版本的实现
应用
1、维护无向图的连通性。支持判断两个点是否在同一连通块内，和判断增加一条边是否会产生环。
2、媒体社交（比如：向通一个社交圈的朋友推荐商品）
3、数学集合（比如：判断元素p,q之后选择是否进行集合合并）
** 常见的一个算法题**， 给出10W 条任何人之间的朋友关系，求这些朋友关系中有多少个朋友圈，并且给出算法的时间复杂度。
样例：
A-B, B -C, D-E, E-F 这 四对关系中存在着两个朋友圈
例题
模板有三个。第一个和第二个已经练习过，但是第三个没有练习过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
1)朴素并查集：
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合：
p[find(a)] = find(b);
(2)维护size的并查集：
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合：
p[find(a)] = find(b);
size[b] += size[a];
(3)维护到祖宗节点距离的并查集：
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[I] = 0;
}
// 合并a和b所在的两个集合：
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量
|
- 547. Friend Circles
p[x] 表示结点 x 的祖先结点，在进行find 之后，找到该节点的祖先结点，这个过程中应用了路径压缩。使用了递归的思想。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
// 这个是并查集中的裸题
vector<int> p;
// 找父节点的一个基本操作
int find(int x)
{
// 根据通项公式（假设）， p[x] 的祖先结点已知
if(p[x] != x) p[x] =find(p[x]); //路径压缩
return p[x];
}
int findCircleNum(vector<vector<int>>& M) {
int n =M.size();
// 初始化，每个节点都是自己的父节点
for(int i =0; i<n; i++) p.push_back(i);
int res =n;
for(int i =0; i< n; i++)
{
for(int j =0; j< i; j++)
{
if(M[i][j] ==0) continue;
if(find(i) !=find(j))
{
p[find(i)] =find(j);
res -=1;
}
}
}
return res;
}
};
|
- 合并集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#include<iostream>
#include<string>
#include<vector>
using namespace std;
vector<int> p;
int find(int x)
{
if( x!= p[x]) p[x] =find(p[x]);
return p[x];
}
int main()
{
int n, m;
cin >>n>>m;
for(int i =0; i<n; i++) p.push_back(i);
while(m --)
{
string s;
int a, b;
cin >> s >>a>> b;
if(s =="M") p[find(a)] =p[find(b)];
if(s =="Q")
{
if(find(a) ==find(b)) cout <<"Yes"<<endl;
else cout<< "No" <<endl;
}
}
return 0;
}
|
- 连通块中点的数量
重点是需要维护一个 size 的数组，这样的话就能得知 每一个连通图的大小。
时空分析：
总的时间复杂度 $O(m +n)$
总的空间复杂度$O(n)$
init 的函数 : $O(n) $
find 函数 $O(logn )$ 可以近似认为是 $O(1)$
merge 函数 $O(1)$
size 函数 $O(1)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#include<iostream>
#include<vector>
using namespace std;
const int N =1e5+11;
int m, n;
vector<int> p;
vector<int> size;
void init()
{
for(int i =0; i<n; i++)
{
p.push_back(i);
size.push_back(1);
}
}
int find(int x)
{
if(x != p[x]) p[x] =find(p[x]);
return p[x];
}
void merge(int x, int y)
{
int t1, t2;
t1 =find(x);
t2 =find(y);
if(t1 != t2)
{
// 规定一律向 x 合并
p[t2] =t1;
size[t1] += size[t2];
}
}
int main()
{
cin >>n >>m;
init();
while( m--)
{
string op;
int a, b;
cin >> op;
if(op =="C")
{
cin >>a>>b;
merge(a, b);
}
else if(op =="Q1")
{
cin >>a>>b;
if(find(a) == find(b) ) puts("Yes");
else puts("No");
}
else
{
// 就是应该单独写，这个条件下只有一个输入
cin >>a;
cout << size[find(a)] <<endl;
}
}
return 0;
}
|
- 684. Redundant Connection
并查集的操作是 $O(1)$ 需要遍历一遍数组，所以总的时间是$O(n)$。
其中有一点，为什么多申请了一个空间，这个是没有很明白的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
vector<int> p;
void init(int n)
{
for(int i =0; i< n; i++)
p.push_back(i);
}
int find(int x)
{
if(x != p[x]) p[x] =find(p[x]);
return p[x];
}
bool is_union(int x, int y)
{
int t1 =find(x);
int t2 =find(y);
if( t1 ==t2) return true;
else
{
p[t1] =p[t2];
return false;
}
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n =edges.size() ;
init(n+1);// 这里为什么要多申请一个空间
cout << n<<endl;
vector<int> res(2, 0);
for(int i =0; i< n; i++)
{
int x =edges[i][0];
int y =edges[i][1];
//cout << x<<" "<< y<< " "<< endl;
if(is_union(x, y))
{
res[0] =x;
res[1] =y;
}
}
return res;
}
};
|
- (784. 强盗团伙)[https://www.acwing.com/problem/content/description/786/]
题解
简单的题解：
此题的朋友的朋友是很好理解的，只要是我的朋友，我们就是一个team，进行Union操作。但是敌人的敌人也是我们的朋友，怎么考量呢？我们需要为此增加一个f数组，存储我的敌人的大哥，很好理解，a和b是敌人的话，b和c是敌人的话，那么a和c应该是一个team的，此处需要对a和c进行Union操作，我们第一次存储的敌人是一个参考，判断哪些人应该合并。
时间复杂分析， sort() 函数是 $O(mlog m)$ ，然后需要遍历一遍边 $O(m)$, 并查集操作一般认为是 $O(1)$，所以最后是 $O(mlog m)$ ，m 表示边的数量。
kruskal 算法求解最小生成树
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
#include<iostream>
#include<algorithm>
using namespace std;
const int N =1e5+11, M =2e5+11, INF =0x3f3f3f3f;
int n, m;
int p[N];
struct Edge
{
int a, b, w;
}edges[M];
int find(int x)
{
// 这个是递归的定义，只需要一次if 就行，不要使用 while
if(p[x] != x) p[x] =find(p[x ]);
return p[x];
}
bool cmp(Edge a, Edge b)
{
return a.w< b.w;
}
int kruskal()
{
sort(edges, edges +m, cmp);
for(int i =1; i<=n; i++) p[i] =i;
int res =0, cnt =0;
for(int i =0; i<m ;i++)
{
int a =edges[i].a, b =edges[i].b, w =edges[i].w;
a =find(a), b =find(b);
if(a !=b)
{
p[a]=b;
res +=w;
cnt ++;
}
}
if (cnt !=n -1) return INF;
return res;
}
int main()
{
cin >> n>>m;
for(int i =0; i<m; i++)
{
int a, b, w;
cin >>a>>b>>w;
edges[i] ={a, b, w};
}
int t =kruskal();
if(t ==INF) puts("impossible");
else cout<<t<<endl;
}
|
参考文献
https://www.cnblogs.com/SeaSky0606/p/4752941.html